DM : Les Suites
29 messages
- Page 1 sur 2 - 1, 2
DM : Les Suites
Bonjour tout le monde !
J'espère que vous avez tous passés de bonnes fêtes et je vous souhaite un tres bonne année 2008 !
Alors voilà j'ai un DM sur les Suites pour lundi et je ne comprends pas grand chose...
Je vous donne l'énoncé puis ce que j'ai fais et mes questions...
Merci d'avance pour votre aide
Aurélie
** ENONCE: **
Ex 1: Un propriétaire propose à partir du 1er janvier 2000 un appartement dont le montant annuel initial du loyer est 30000F.Il envisage deux types d'augmentation.
1) Dans le premier cas, le loyer annuel augmenterait de chaque année de 1000F.
On désigne par Pn le montant annuel du loyer pour l'année (2000+n); on a donc P[/sub]n = 30000.
a)Calculer P[sub]1 et P2
b)Montrer que Pn est une suite arithmétique.Déterminez sa raison.
c)Exprimer Pn enfonction de n.
d)Quel serait le montant annuel en 2015 arrondi au franc près?
e)En quelle année le loyer dépassera t'il le double du loyer initial ?
f)Quelle serait la somme perçue par le propriétaire au terme des vingt premières années
(on donnera la valeur arrondie au millier de francs)?
** MON RAISONNEMENT + QUESTIONS **
a) Récapitulatif: P0= Montant annuel du loyer pour l'année 2000 = 30000F
P1= Montant annuel du loyer pour l'année 2001
P2= Montant annuel du loyer pour l'année 2002
P1= P0+1000
= 30000+1000=31000
-> Le montant annuel du loyer pour l'année 2001 sera de 31000F
P2= P0+(1000x2) P2=P1+1000
= 30000+2000 OU: =31000+1000
= 32000 =32000
-> Le montant annuel du loyer pour l'année 2002 sera de 32000F
( Est-ce -quec'est juste ?Et la présentation,c'est bon ?)
b)
(je ne sais pas comment montrer que (PN) est une Suite arithmétique!
c'est parcequ'il y a le signe + non ?il faut seulement dire ça ?)
(PN) est une Suite Arithmétique de raison r=1000
(Est-ce-que c'est ça ?)
c)(PN)est définie par: PN= P0+(1000xn)
d) P2015= P0+(1000x15)
P2015= 30000+15000
P2015= 45000
-> Le montant annuel du loyer pour l'année 2015 sera de 45000F
e)Le loyer dépassera le double du loyer initial lorsque Pn > P0x2
PN= 30000 + (1000 x n)
Pour connaitre il faut résoudre l'équation suivante:
30000+(1OOO x n)= 60000
30000+1000n=60000
1000n=60000-30000=30000
n=30000/1000=30
Donc: P30= 30000 + (1000 x 30)
P30= 30000 + 30000
P30= 60000
-> En 2030, le loyer sera le double qu'en 2000
Donc,le loyer dépassera le double du loyer initial à partir de 2031.
f)P20= 30000 + (1000x20)
P20= 30000 + 20000
P20= 50000
-> La somme perçue par le propriétaire au terme des vingt premières années serait de 50000F.
**** voila le 1 du premier exercice! je n'ai pas encore fais le 2 mais voilà déja ça !
Merci de me dire si c'est juste ou pas et de me dire si la présentation est bonne telle qu'elle est.
Bonne soirée
Aurélie
J'espère que vous avez tous passés de bonnes fêtes et je vous souhaite un tres bonne année 2008 !
Alors voilà j'ai un DM sur les Suites pour lundi et je ne comprends pas grand chose...
Je vous donne l'énoncé puis ce que j'ai fais et mes questions...
Merci d'avance pour votre aide
Aurélie
** ENONCE: **
Ex 1: Un propriétaire propose à partir du 1er janvier 2000 un appartement dont le montant annuel initial du loyer est 30000F.Il envisage deux types d'augmentation.
1) Dans le premier cas, le loyer annuel augmenterait de chaque année de 1000F.
On désigne par Pn le montant annuel du loyer pour l'année (2000+n); on a donc P[/sub]n = 30000.
a)Calculer P[sub]1 et P2
b)Montrer que Pn est une suite arithmétique.Déterminez sa raison.
c)Exprimer Pn enfonction de n.
d)Quel serait le montant annuel en 2015 arrondi au franc près?
e)En quelle année le loyer dépassera t'il le double du loyer initial ?
f)Quelle serait la somme perçue par le propriétaire au terme des vingt premières années
(on donnera la valeur arrondie au millier de francs)?
** MON RAISONNEMENT + QUESTIONS **
a) Récapitulatif: P0= Montant annuel du loyer pour l'année 2000 = 30000F
P1= Montant annuel du loyer pour l'année 2001
P2= Montant annuel du loyer pour l'année 2002
P1= P0+1000
= 30000+1000=31000
-> Le montant annuel du loyer pour l'année 2001 sera de 31000F
P2= P0+(1000x2) P2=P1+1000
= 30000+2000 OU: =31000+1000
= 32000 =32000
-> Le montant annuel du loyer pour l'année 2002 sera de 32000F
( Est-ce -quec'est juste ?Et la présentation,c'est bon ?)
b)
(je ne sais pas comment montrer que (PN) est une Suite arithmétique!
c'est parcequ'il y a le signe + non ?il faut seulement dire ça ?)
(PN) est une Suite Arithmétique de raison r=1000
(Est-ce-que c'est ça ?)
c)(PN)est définie par: PN= P0+(1000xn)
d) P2015= P0+(1000x15)
P2015= 30000+15000
P2015= 45000
-> Le montant annuel du loyer pour l'année 2015 sera de 45000F
e)Le loyer dépassera le double du loyer initial lorsque Pn > P0x2
PN= 30000 + (1000 x n)
Pour connaitre il faut résoudre l'équation suivante:
30000+(1OOO x n)= 60000
30000+1000n=60000
1000n=60000-30000=30000
n=30000/1000=30
Donc: P30= 30000 + (1000 x 30)
P30= 30000 + 30000
P30= 60000
-> En 2030, le loyer sera le double qu'en 2000
Donc,le loyer dépassera le double du loyer initial à partir de 2031.
f)P20= 30000 + (1000x20)
P20= 30000 + 20000
P20= 50000
-> La somme perçue par le propriétaire au terme des vingt premières années serait de 50000F.
**** voila le 1 du premier exercice! je n'ai pas encore fais le 2 mais voilà déja ça !
Merci de me dire si c'est juste ou pas et de me dire si la présentation est bonne telle qu'elle est.
Bonne soirée
Aurélie
salut,
oui, ça va
c'est pas suffisant
Le loyer pour l'année 2000 est P0=30000.Le loyer augmente de 1000 chaque année, on a donc
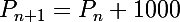 , ce qui montre que la suitre Un est une suite arithmetique de 1er terme P0=30000 et de raison 1000
, ce qui montre que la suitre Un est une suite arithmetique de 1er terme P0=30000 et de raison 1000
ok
ok
faux il faut que tu utilises la formule de la somme des n premier terme d'une suite arithmetique de raison ici 1000 et de 1er terme P0=30000
rappel
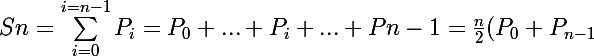)
a) Récapitulatif: P0= Montant annuel du loyer pour l'année 2000 = 30000F
P1= Montant annuel du loyer pour l'année 2001
P2= Montant annuel du loyer pour l'année 2002
P1= P0+1000
= 30000+1000=31000
-> Le montant annuel du loyer pour l'année 2001 sera de 31000F
P2= P0+(1000x2) P2=P1+1000
= 30000+2000 OU: =31000+1000
= 32000 =32000
-> Le montant annuel du loyer pour l'année 2002 sera de 32000F
( Est-ce -quec'est juste ?Et la présentation,c'est bon ?)
oui, ça va
b)
(je ne sais pas comment montrer que (PN) est une Suite arithmétique!
c'est parcequ'il y a le signe + non ?il faut seulement dire ça ?)
(PN) est une Suite Arithmétique de raison r=1000
(Est-ce-que c'est ça ?)
c'est pas suffisant
Le loyer pour l'année 2000 est P0=30000.Le loyer augmente de 1000 chaque année, on a donc
okc)(PN)est définie par: PN= P0+(1000xn)
d) P2015= P0+(1000x15)
P2015= 30000+15000
P2015= 45000
-> Le montant annuel du loyer pour l'année 2015 sera de 45000F
ok
e)Le loyer dépassera le double du loyer initial lorsque Pn > P0x2
PN= 30000 + (1000 x n)
Pour connaitre il faut résoudre l'équation suivante:
30000+(1OOO x n)= 60000
30000+1000n=60000
1000n=60000-30000=30000
n=30000/1000=30
Donc: P30= 30000 + (1000 x 30)
P30= 30000 + 30000
P30= 60000
-> En 2030, le loyer sera le double qu'en 2000
Donc,le loyer dépassera le double du loyer initial à partir de 2031.
ok
f)P20= 30000 + (1000x20)
P20= 30000 + 20000
P20= 50000
-> La somme perçue par le propriétaire au terme des vingt premières années serait de 50000F.
faux il faut que tu utilises la formule de la somme des n premier terme d'une suite arithmetique de raison ici 1000 et de 1er terme P0=30000
rappel
Recoucou ! :)
Alors voilà la fin du premier exercice (le petit 2):
*** ENONCE ***
Dans le deuxième cas, le loyer annuel augmenterait de chaque année 3%.
On désigne par Qn le montant annuel du loyer pour l'année (2000+n) ; on a donc Qn= 30000.
a) Calculer Q1 et Q2.
b)Montrer que (Qn) est uen suite géométrique.Déterminer sa raison.
c)Exprimer Qn en fonction de n.
d)QUel serait le montant annuel du loyer ne 2015,arrondi au franc près?
e)En quelle année le loyer dépassera-t-il le double du loyer initial ?(a l'aide de la calculatrice)
f)Quelle serait la somme perçue par le propriétaire au terme des vingt premières années (on donnera la valeur arrondie au millier de francs)?
***MON RAISONNEMENT+ QUESTIONS***
a) Récapitulatif:
Q0= Montant annuel du loyer pour l'année 2000 = 30000F
Q1= Montant annuel du loyer pour l'année 2001
Q2= Montant annuel du loyer pour l'année 2002
Q1= 30000+ (30000 x (3 /100 ) )
= 30900
-> Le montant annuel du loyer pour l'année 2001 sera de 30900F
Q2=30000 + (Q1 x 3/100)
=30000 +(30900x 0,03)
= 30000 + 927
= 30927
-> Le montant annuel du loyer pour l'année 2002 sera de 30927F
b) Le loyer pour l'année 2000 est P0=30000.Le loyer augmente de 3% chaque année, on a donc:
Pn+1= Pn x (3/100), ce qui montre que la suite Pn est une suite géometrique de premier terme P0=30000 et de raison 3/100.
c) (Qn) est définie par: Qn=Q0+(Qn-1 x 3/100 )
d) P2015=P0+(P2014 x 3/100)
Comment calculer 2014 ?
je pense que je me suis trompée pour calculer Qn et tout...
pouvez vous me dire si j'ai juste ou pas avant que je fasse le e) et f) ?
MERCII !! :we:
Alors voilà la fin du premier exercice (le petit 2):
*** ENONCE ***
Dans le deuxième cas, le loyer annuel augmenterait de chaque année 3%.
On désigne par Qn le montant annuel du loyer pour l'année (2000+n) ; on a donc Qn= 30000.
a) Calculer Q1 et Q2.
b)Montrer que (Qn) est uen suite géométrique.Déterminer sa raison.
c)Exprimer Qn en fonction de n.
d)QUel serait le montant annuel du loyer ne 2015,arrondi au franc près?
e)En quelle année le loyer dépassera-t-il le double du loyer initial ?(a l'aide de la calculatrice)
f)Quelle serait la somme perçue par le propriétaire au terme des vingt premières années (on donnera la valeur arrondie au millier de francs)?
***MON RAISONNEMENT+ QUESTIONS***
a) Récapitulatif:
Q0= Montant annuel du loyer pour l'année 2000 = 30000F
Q1= Montant annuel du loyer pour l'année 2001
Q2= Montant annuel du loyer pour l'année 2002
Q1= 30000+ (30000 x (3 /100 ) )
= 30900
-> Le montant annuel du loyer pour l'année 2001 sera de 30900F
Q2=30000 + (Q1 x 3/100)
=30000 +(30900x 0,03)
= 30000 + 927
= 30927
-> Le montant annuel du loyer pour l'année 2002 sera de 30927F
b) Le loyer pour l'année 2000 est P0=30000.Le loyer augmente de 3% chaque année, on a donc:
Pn+1= Pn x (3/100), ce qui montre que la suite Pn est une suite géometrique de premier terme P0=30000 et de raison 3/100.
c) (Qn) est définie par: Qn=Q0+(Qn-1 x 3/100 )
d) P2015=P0+(P2014 x 3/100)
Comment calculer 2014 ?
je pense que je me suis trompée pour calculer Qn et tout...
pouvez vous me dire si j'ai juste ou pas avant que je fasse le e) et f) ?
MERCII !! :we:
re,
pas tout à fait d'accord
on te dit que le Loyer augmente de 3% chaque année donc:
pour l'année 2000 il est de 30000=Q0
pour l'année 2001 il est de 30000+30000*3/100=Q0+Q0*3/100=30900=P1
pour l'année 2002 il est de 30900+30900*3/100=Q1+Q1*3/100=31827
b) Si le loyer pour l'année 2000+n est Pn avec(Q0=30000), le loyer pour l'année suivante est :
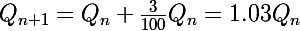
la suite Qn est une suite geometrique de raison 1.03 et de 1er terme Q0=30000
ok jusqu'ici ?
essaie de revoir la question c) et d)
a) Récapitulatif:
Q0= Montant annuel du loyer pour l'année 2000 = 30000F
Q1= Montant annuel du loyer pour l'année 2001
Q2= Montant annuel du loyer pour l'année 2002
Q1= 30000+ (30000 x (3 /100 ) )
= 30900
-> Le montant annuel du loyer pour l'année 2001 sera de 30900F
Q2=30000 + (Q1 x 3/100)
=30000 +(30900x 0,03)
= 30000 + 927
= 30927
-> Le montant annuel du loyer pour l'année 2002 sera de 30927F
b) Le loyer pour l'année 2000 est P0=30000.Le loyer augmente de 3% chaque année, on a donc:
Pn+1= Pn x (3/100), ce qui montre que la suite Pn est une suite géometrique de premier terme P0=30000 et de raison 3/100.
pas tout à fait d'accord
on te dit que le Loyer augmente de 3% chaque année donc:
pour l'année 2000 il est de 30000=Q0
pour l'année 2001 il est de 30000+30000*3/100=Q0+Q0*3/100=30900=P1
pour l'année 2002 il est de 30900+30900*3/100=Q1+Q1*3/100=31827
b) Si le loyer pour l'année 2000+n est Pn avec(Q0=30000), le loyer pour l'année suivante est :
la suite Qn est une suite geometrique de raison 1.03 et de 1er terme Q0=30000
ok jusqu'ici ?
essaie de revoir la question c) et d)
Ah d'accord ! j'étais repartie du terme Q0 et non de Q1!!
Merci beaucoup !
Oui j'ai compris, j'ai réécris sur papier,ça m'aide (d'où le temps entre chaque réponse ;) )
Désolée pour le temps de la réponse j'ai du m'absenter ! :s
Alors pour la c) : :happy2:
Qn = 30 000 ×1,03^n
et pour la d) :
Q2015 = 30 000 x 1,03^2015
= 30 000 x ...
euh.. c'est ça ? ça me met un chiffre en écriture scientifique...
Merci beaucoup !
Oui j'ai compris, j'ai réécris sur papier,ça m'aide (d'où le temps entre chaque réponse ;) )
Désolée pour le temps de la réponse j'ai du m'absenter ! :s
Alors pour la c) : :happy2:
Qn = 30 000 ×1,03^n
et pour la d) :
Q2015 = 30 000 x 1,03^2015
= 30 000 x ...
euh.. c'est ça ? ça me met un chiffre en écriture scientifique...
Ah oui tu as raison !!! ^^ :marteau: lol
c'est vrai moi non plus :)
Pour la e) j'ai un problème! (encore) :
Le loyer dépassera le double du loyer initial lorsque Qn > P0 x 2
Qn = 30000 X 1,03^n
Pour connaitre n, il faut résoudre l'équation suivante:
30000 x 1,03^n = 60000
1,03^n = 60000/30000
1,03^n= 2
...je ne vois pas comment trouver la puissance n .. :s
c'est vrai moi non plus :)
Pour la e) j'ai un problème! (encore) :
Le loyer dépassera le double du loyer initial lorsque Qn > P0 x 2
Qn = 30000 X 1,03^n
Pour connaitre n, il faut résoudre l'équation suivante:
30000 x 1,03^n = 60000
1,03^n = 60000/30000
1,03^n= 2
...je ne vois pas comment trouver la puissance n .. :s
29 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
