Somme des racines d'un polynomes

[theblinker]

Bonjour a tous,

je suis en prepa HEC 1ere année

je suis bloqué sur deux questions , et j'aurrais fini mon 1er DM de l'année!!!

voici l'énoncé
soit P=anX^n+an-1X^n-1+....+a0 un polynome à coefficients réels possèdant n racines réelles x1,...,xn
j'ai démontrer x1+x2+...+xn=-(an-1)/an

--soit x€R montrer qu'il existe une suite de polynomes Pn € r[X] telle que:
pour tout n €N* sin((2n+1)x)=Pn(cot²x)sin^(2n+1) (x)

jai éssayer de transfomer avec les formules de trigo mais en le faisant 3 fois je trouve 3fois des resultats differents!!

--démontrer que les racines de Pn sont x1,...xn ou on a posé
pour tout k compris (sens large) entre 1 et n , xk=cot²((kpi)/(2n+1)
euh cette question je ne sait trop quoi faire j'ai beaucoup de mal....!

Merci d'avance pour votre aide
Et bonne année!!

[busard_des_roseaux]

bjr,

je m'excuse, je n'ai pas trop de temps de faire les calculs. Voilà les grandes lignes:



avec =partie imaginaire de z

On développe par la formule du binome la dernière expression, en ne gardant que les termes imaginaires purs,ie, les termes de la forme:




Ensuite, on met en facteur ..et l'on tombe sur le résultat.

question 2:

Le polynome est sous la forme d'un quotient. Ses zéros sont obtenus
avec les valeurs qui annulent sin((2n+1)x) , composées avec la fonction .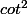

désolé de ne pas t'aider plus.

cordialement,