Une suite de points

[sofye]

bonjour j'ai un probleme avec un exercice :
Le plan complexe est muni d'un repère orthonormal (O;OU;OV).

On considère la suite de points (Mn), n N et la suite des affixes (Zn) n N définie par :

Z0 = 8 et pour tout n de N, Zn+1 = ((1+i racine de 3) Zn )/ 4

3.a) Calculer le rapport (Zn+1 – Zn) / Zn+1

b) En déduire que le triangle OMnMn+1 est rectancle et que |Zn+1 - Zn| = racine de 3 |Zn+1|


Pour la a) je trouve i racine de 3, mais ensuite je bloque totalement

merci d'avance

[fonfon]

salut je n'ai pas fais le calcul mais si tu trouves iV3 que peux tu dire si tu passe à l'argument ....

ensuite si tu as

et que ensuite tu fais

[sofye]

arg(iracine de 3) = pi/2 [2pi] qu'il soit rectangle
mais je ne comprends pas pourquoi

je pense qu'on trouve ça mais je ne vois pas comment

[fonfon]

eh ben

et tu ne reconnais pas un certain angle dans
c'est l'angle...

[sofye]

je sais que c'est l'angle mais comment on sait que arg(i racine de 3) vaut pi / 2 ?

[fonfon]

ben en fait tu as dû le voir dans ton cours avec un schema je pense quand tu traces un repere l'axe des ordonnées c'est l'axe des imaginaires pur donc si tu prends le point A ( par exemple) de coordonnée (0,i) alors on a Arg(i) c'est l'angle formé par le vecteur et le vecteur \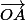 c'est donc on voit que ça forme un angle de

j'ai fait un magnifique dessin pour illustrer mais faut que tu t'approches de l'ecran



j'espere avoir été clair

[sofye]

merci. ça m'a beaucoup aidé.
oui c'était très cler!

[fonfon]

tant mieux si tu as compris