S.groupes de Z^n

[Mohamed]

bonsoir...

comment mq que tt s.groupe de Z^n est isomorphe à Z^r tq 1=
merci pr votre aide..

M+

[ThSQ]

Une suggestion :

Un sous-groupe de Z est {0} ou aZ isomorphe à Z (ça porte un nom les groupes dont tous les sous-groupes propres != {e} sont isomorphes au groupe ?).

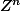
Si G est un sous-groupe de il est de la forme avec Gi ~ {0} ou Z

r = nombre de i tq

[yos]

Hum... un sous groupe de est pas nécessairement de la forme ...
Faut y aller à la main.

[ThSQ]

un sous groupe de est pas nécessairement de la forme ...

Entièrement d'accord ... c'est pas non plus ce que j'ai dit :hein:

[yos]

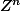
Un sous-groupe de Z est {0} ou aZ isomorphe à Z. Si G est un sous-groupe de il est de la forme avec Gi ~ {0} ou Z

C'est ce que j'avais compris dans les termes ci-dessus.
Pour Mohamed : je veux dire par exemple que les couples (k,3k) de Z² forment un sous-groupe de Z². Il n'est pas de la forme aZxbZ. Il est cependant isomorphe à Z par mais il est pas immédiat que c'est vrai pour tous les sous groupes de Z². Il faut s'inspirer de la preuve du théorème sur les sous-groupes de Z.

[aviateurpilot]

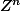
Si G est un sous-groupe de il est de la forme avec Gi ~ {0} ou Z

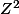
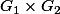
tu veux dire que Si G est un sous-groupe de il est de la forme avec ne sont pas ofrcement des s.g de Z.
mais malheureusement ne peut pas prendre cette forme.

voila se que je vois
soit un s.g de
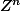
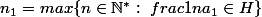
soit soit on prend donc .
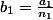
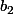
si on construit de la meme facon avec
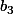
de meme si on construit avec
...
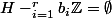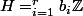
avec ce alogorithme on arret forcement à une -eme etape ou on trouve et dans ce cas et on a (resultat evident)
d'ou il exist l'isomorphisme tel que

N.B: j'ai pas montrer que l'algorithme arret a une etape r car c'est evident mais si vous voulais que je le montrer dis le.

[yos]

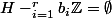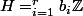
avec ce alogorithme on arret forcement à une -eme etape ou on trouve et dans ce cas et on a (resultat evident)
N.B: j'ai pas montrer que l'algorithme arret a une etape r car c'est evident mais si vous voulais que je le montrer dis le.

Je pense au contraire que ton algorithme s'arrète pas. En tout cas pas en moins de n étapes.
Tu veux un contre-exemple?

[aviateurpilot]

oui, merci

[yos]

u=(1,3), v=(2,2), G=.
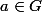
Tu pars de a=(3,5) ( car a=u+v), puis (b=u-v).
Remarque alors que H= est un sous-groupe strict de G (en effet, ).

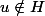
[aviateurpilot]

merci yos, pour le contre exemple
mais au moins je pense qu'on peux ecrire n'importe kel s.g sous la forme il faut seuelemn,t trouvé une facon pour construire ces sauf si tu as un autre contre exemple, lool
merci de tt facon :we:

[yos]

mais au moins je pense qu'on peux ecrire n'importe kel s.g sous la forme

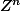
Oui ça marche. C'est parce que est un Z-module libre de rang fini et à ce titre, ses sous-modules sont également libres et de rang .

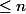
libre = qui possède une base.
rang = cardinal d'une base (elles ont toutes le même cardinal quand l'anneau de base est commutatif, ici c'est Z).

Bref, c'est un exo de cours et tu peux trouver la preuve partout.