Bonjour j'aurais besoin de votre aide s'il vous plait pour résoudre un exercice
Soit f une fonction continue sur [0,+inj[ dérivable sur ]0,+inj[ tel que f(0)=0
et f' est croissante sur ]0,+inj[
Montrer que g défini par g(x)=f(x)/x est croissante
(Appliquer le théorème des accroissements finis)
Pourriez vous m'aider s'il vous plait, je n'arrive pas à comprendre ce que je dois faire car dans le théorème des accroissements finis on travaille sur [a,b] et ici c'est [0,+inf[
merci
Accroissement fini
10 messages
- Page 1 sur 1
Salut aviateurpilot
merci pour ta réponse si çà te dérange pas je peux te demander 2 3 choses s'il te plait
pourrais tu m'expliquer pourquoi et comment tu fais pour distinguer le cas où
a appartient à [0,x]
et
b appartient à [x,y]
tu mets y comme si c'était plus l'infini?
pourquoi x peut être égale à y mais pas à 0?
Sinon pour la suite je comprends ce que tu fais
merci
merci pour ta réponse si çà te dérange pas je peux te demander 2 3 choses s'il te plait
pourrais tu m'expliquer pourquoi et comment tu fais pour distinguer le cas où
a appartient à [0,x]
et
b appartient à [x,y]
tu mets y comme si c'était plus l'infini?
pourquoi x peut être égale à y mais pas à 0?
Sinon pour la suite je comprends ce que tu fais
merci
on veux montrer que g est coissante sur 
pou montre cela, on fixe x et y dans (N.B: y est un reél fixé et pas l'infini !!!) tel que
(N.B: y est un reél fixé et pas l'infini !!!) tel que 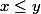 et puis on montre que
et puis on montre que \le g(y) )
)
j'ai ecrit donc "soit "
"
th des acroiss fini sur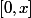 donne
donne -f(0)=(x-0)f'(a))
th des acroiss fini sur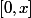 donne
donne -f(0)=(x-0)f'(a))
-f(x)=(x-y)f'(b))
donc il est evident que\le f'(x)\le f'(b))
ce qui suit ne sont que des calcules
=f(x)+(x-y)f'(b)=xf'(a)+(x-y)f'(b)\ge (x+(y-x))f'(a)=yf'(a)=xyf(x))
d'ou=\frac{f(y)}{y}\ge \frac{xyf(x)}{y}=g(x)) [/quote]
[/quote]
pou montre cela, on fixe x et y dans
j'ai ecrit donc "soit
th des acroiss fini sur
th des acroiss fini sur
donc il est evident que
ce qui suit ne sont que des calcules
d'ou
log86 a écrit:Bonjour j'aurais besoin de votre aide s'il vous plait pour résoudre un exercice
Soit f une fonction continue sur [0,+inj[ dérivable sur ]0,+inj[ tel que f(0)=0
et f' est croissante sur ]0,+inj[
Montrer que g défini par g(x)=f(x)/x est croissante
(Appliquer le théorème des accroissements finis)
Pourriez vous m'aider s'il vous plait, je n'arrive pas à comprendre ce que je dois faire car dans le théorème des accroissements finis on travaille sur [a,b] et ici c'est [0,+inf[
merci
Bonjour,
Par convexité c'est immédiat non?
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
