Idéaux maximaux
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
SimonB
 par SimonB » 20 Déc 2007, 22:14
par SimonB » 20 Déc 2007, 22:14
Bonsoir,
Je travaille dans
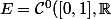)
. Je dois prouver que si f appartient à un idéal maximal I de E, f s'annule en au moins un point de [0,1]. Je ne vois pas du tout par où commencer : je pense qu'il faudrait exploiter la définition d'un idéal maximal (s'il existe un idéal le contenant, cet idéal est l'anneau de départ) en construisant par l'absurde un idéal plus grand qui ne serait pas E tout entier. Mais comment faire ?
(La suite de l'exercice consiste à prouver que des fonctions (f1, f2, ..., fp) qui appartiennent à un idéal maximal s'annulent en au moins un point commun, puis que les idéaux maximaux de E sont nécessairement de la forme
=0})
(question pour laquelle je pense qu'il va falloir utiliser Borel-Lebesgue, version compacts...))
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 20 Déc 2007, 22:30
par abcd22 » 20 Déc 2007, 22:30
Bonjour,
Si f ne s'annule pas, elle est inversible dans l'anneau considéré...
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 20 Déc 2007, 22:32
par ThSQ » 20 Déc 2007, 22:32
Intéressant :we:
Une suggestion pour la suite de l'exo :
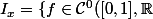 | f(x) = 0 \})
est un idéal.
Si f ne s'annule nulle part l'idéal I est différent des I_x pour tout x (on ne peut pas avoir

par maximalité).
Donc pour tout x, il y a une
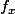
tq
 \neq 0)
.
Par continuité f ne s'annule par sur V_x un voisinage. Les V_x recouvre [0;&] compact, on prend un recouvrement fini :
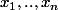
et

. F ne s'annule jamais et donc est inversible. Le pb c'est que

c'est gênant pour un idéal d'avoir un élément inversible :ruse:
-
SimonB
 par SimonB » 20 Déc 2007, 22:46
par SimonB » 20 Déc 2007, 22:46
Suis-je bête ! Merci beaucoup, je n'avais pas pensé à cette propriété élémentaire ;)
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 21 Déc 2007, 09:51
par yos » 21 Déc 2007, 09:51
bonjour.
S'il existe deux éléments f,g de I sans zéro commun, alors I contient f²+g² , comme l'a dit thsq; mais f²+g² inversible, impossible. A-t-on besoin de la compacité?
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 21 Déc 2007, 14:56
par ThSQ » 21 Déc 2007, 14:56
Ca y est c'est la vacances :rulaiz: je vais enfin pouvoir regarder de près les Sylow :crunch:, euh, je veux dire me reposer .
Yos je pense que la compacité (ou une condition moins forte à trouver ?) est indispensable si l'on veut montrer que les
idéaux maximaux de
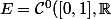)
sont les
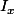
(avec mes notations) ( mais elle est pas utile pour montrer que f d'un idéal propre s'annule bien sûr).
Je crois que j'ai un contrex-vittel dans le cas
non compact.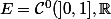)
.
I = { f | f s'annule sur ]0, 1/n[ pour un n donné }. I est un idéal.
I est contenu dans un idéal maximal M. Si M = I_x pour un certain x on a un contradiction en prenant n = 1/(x+1).
Compact est suffisant. Sûrement pas nécessaire mais faudrait trouver un exemple .... :help:
 par busard_des_roseaux » 21 Déc 2007, 16:31
par busard_des_roseaux » 21 Déc 2007, 16:31
bjr ThQs,
La discussion, avec les arguments des uns et des autres, semble OK.
Soit I un idéal maximal de
)
S'il existe

ne s'annulant pas, I=A.
Sinon


car la fonction constante = 1
n'appartient pas à

donc

puisque I est supposé maximal.
La compacité n'est pas utilisée.
cordialement,

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 21 Déc 2007, 16:46
par leon1789 » 21 Déc 2007, 16:46
busard_des_roseaux a écrit:bjr ThQs,
La discussion, avec les arguments des uns et des autres, semble OK.
heu, je ne suis pas de cet avis :we:
busard_des_roseaux a écrit:Soit I un idéal maximal de
)
S'il existe

ne s'annulant pas, I=A.
Sinon

heu pourquoi ? ( l'idéal I n'est pas engendré par f...)
ThSQ a écrit:Je crois que j'ai un contrex-vittel dans le cas
non compact.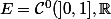)
.
I = { f | f s'annule sur ]0, 1/n[ pour un n donné }. I est un idéal.
I est contenu dans un idéal maximal M. Si M = I_x pour un certain x on a un contradiction en prenant n = 1/(x+1).
Mais tu changes d'idéal I en fonction de l'idéal M !
Ton idéal I (pour n fixé) est inclus dans

-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 21 Déc 2007, 16:51
par yos » 21 Déc 2007, 16:51
J'ai mal lu le premier message de Thsq (qui a raison je pense).
Si on a une famille infinie de fonctions (f_i) dans l'idéal, on peut pas lui appliquer la somme des carrés.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 21 Déc 2007, 16:53
par leon1789 » 21 Déc 2007, 16:53
ThSQ a écrit:(...)
Donc pour tout x, il y a une
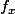
tq
 \neq 0)
.
Par continuité f ne s'annule par sur V_x un voisinage. Les V_x recouvre [0;1] compact, on prend un recouvrement fini :
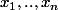
et

. F ne s'annule jamais et donc est inversible.
ok, j'ai compris...
Les idéaux
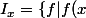 = 0\})
sont maximaux : ok.
Soit I un idéal contenu dans aucun des
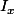
, c'est à dire que pour tout x, il existe

et
 \neq 0)
.
Puis le truc de compacité de ThSQ, et enfin la fonction

et F inversible, donc I = l'anneau.
Cela montre effectivement que les
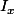
sont LES idéaux maximaux. Ok
Bien joué ThSQ !
ThSQ a écrit:Le pb c'est que

c'est gênant pour un idéal d'avoir un élément inversible :ruse:
Ben non, je ne trouve pas : ça permet de connaitre l'idéal comme ça :we:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 21 Déc 2007, 16:54
par yos » 21 Déc 2007, 16:54
leon1789 a écrit:Mais tu changes d'idéal I en fonction de l'idéal M !
[/TEX]
Non c'est OK : I est l'ensemble des fonctions telles qu'il existe un n vérifiant

.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 21 Déc 2007, 18:17
par leon1789 » 21 Déc 2007, 18:17
yos a écrit:Non c'est OK : I est l'ensemble des fonctions telles qu'il existe un n vérifiant
=0)
.
Ah ok ! (c'était bien écrit, j'avais mal lu...)
Re-bien joué ThSQ !
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 21 Déc 2007, 18:29
par yos » 21 Déc 2007, 18:29
L'exo est assez mal posé non?
J'aurais dit :
1) Soit I idéal propre de A. Alors
a) tout f de I s'annule.
b) toute famille finie de I s'annule.
c) toute famille infinie de I s'annule.
2) Soit I idéal maximal de I. Alors I=...
-
SimonB
 par SimonB » 21 Déc 2007, 18:31
par SimonB » 21 Déc 2007, 18:31
Borel-Lebesgue pouvant s'énoncer également avec des compacts, on peut aussi dire : Pour toute famille finie de fonctions f appartenant à I, l'intersection des

est non vide, donc l'idéal est bien de la forme recherchée. Je trouve ça un peu plus simple...
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 21 Déc 2007, 19:22
par ThSQ » 21 Déc 2007, 19:22
SimonB a écrit:Borel-Lebesgue pouvant s'énoncer également avec des compacts
?? C'est quoi Borel-Lebesgue pour toi ?
Sinon, des idées de condition suffisante à part la compacité ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 21 Déc 2007, 19:41
par leon1789 » 21 Déc 2007, 19:41
yos a écrit:L'exo est assez mal posé non?
J'aurais dit :
1) Soit I idéal propre de A. Alors
a) tout f de I s'annule.
b) toute famille finie de I s'annule.
c) toute famille infinie de I s'annule.
2) Soit I idéal maximal de I. Alors I=...
Comment aurais-tu démontrer les réponses à ces questions ? par l'absurde ? :marteau:
Je trouve bien cet énoncé :
1) Quels sont les inversibles de l'anneau ?
2) Montrer que les idéaux
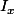
sont maximaux.
3) Montrer que des fonctions

sont globalement comaximales ssi elles sont sans zéro commun.
4) Soit

un idéal évitant tous les idéaux
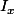
.
Montrer que I contient un inversible. (utiliser la continuité et la compacité)
5) Conclure.
-
BiZi
- Membre Relatif
- Messages: 307
- Enregistré le: 26 Mai 2006, 21:06
-
 par BiZi » 21 Déc 2007, 19:53
par BiZi » 21 Déc 2007, 19:53
abcd22 a écrit:Bonjour,
Si f ne s'annule pas, elle est inversible dans l'anneau considéré...
Pardonnez mon ignorance, mais pourquoi? :hum:

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 21 Déc 2007, 19:55
par leon1789 » 21 Déc 2007, 19:55
BiZi a écrit:Pardonnez mon ignorance, mais pourquoi? :hum:
"inversible" au sens de la multiplication (pas de la composition)
Un élément de R est inversible ssi il est non nul. Une fonction est inversible ssi elle ne s'annule pas. son inverse est alors 1/f
-
BiZi
- Membre Relatif
- Messages: 307
- Enregistré le: 26 Mai 2006, 21:06
-
 par BiZi » 21 Déc 2007, 20:00
par BiZi » 21 Déc 2007, 20:00
leon1789 a écrit:"inversible" au sens de la multiplication (pas de la composition)
Un élément de R est inversible ssi il est non nul. Une fonction est inversible ssi elle ne s'annule pas. son inverse est alors 1/f
Oups en effet heureusement que c'est les vacances :marteau: Merci!
 par busard_des_roseaux » 21 Déc 2007, 20:07
par busard_des_roseaux » 21 Déc 2007, 20:07
-------------------------------------------------
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
ne s'annulant pas, I=A.
.
tq
.
et
. F ne s'annule jamais et donc est inversible.
c'est gênant pour un idéal d'avoir un élément inversible :ruse: