bonsoir a tous
voila,je dois repondre a cette question :
determiner les fonctions f continues sur R telles que
f(x) + ( integrale (x+t)*f(x-t)dt entre 0 et x ) = 1
alors,j'ai fait un changement de variable,u=x-t,et j'ai dérivé 2 fois (f est clairement deux fois derivables),et j'obtiens
f''(x) + x*f'(x) + 3*f(x) = 1
comment resoudre cette equation ?
merci !!
Equation différentielle
5 messages
- Page 1 sur 1
par isortoq » 20 Déc 2007, 10:44
maxboubou a écrit:bonsoir a tous
voila,je dois repondre a cette question :
determiner les fonctions f continues sur R telles que
f(x) + ( integrale (x+t)*f(x-t)dt entre 0 et x ) = 1
alors,j'ai fait un changement de variable,u=x-t,et j'ai dérivé 2 fois (f est clairement deux fois derivables),et j'obtiens
f''(x) + x*f'(x) + 3*f(x) = 1
comment resoudre cette equation ?
merci !!
Bonjour !
Ce devrait être : f''(x) + x*f'(x) + 3*f(x) = 0
et ensuite je crois qu'on peut en trouver 2 solutions linéairement indépendantes en les cherchant sous la forme d'une série entière...
par busard_des_roseaux » 20 Déc 2007, 15:14
bjr,
La démonstration est assez longue,désolé.
en faisant le changement de variable u=x-t, on trouve:
+2x \int_{0}^{x} \, f(u)du - \int_{0}^{x} uf(u)du =1)
(E1)
on en déduit que f est indéfiniment dérivable et f(0)=1.
En dérivant l'égalité E1, on obtient:
+xf(x)+2\int_{0}^{x} \, f(u)du=0)
(E2)
d'où f'(0)=0.
En dérivant l'égalité (E2), on montre par récurrence sur l'entier n que:
}(x)+xf^{(n-1)}(x)+(n+1)f^{(n-2)}(x)=0)
soit
}(0)=-(n+1)f^{(n-2)}(0))
d'où
}(0)=0 \forall n \in \mathbb{N})
}(0)={(-1)}^n \frac{(2n+2)!}{2^{n+1}(n+1)!} \forall n \in \mathbb{N})
En écrivant f comme somme de sa série de Taylor en l'origine:
=\sum_{n \geq 0} {(-1)}^n \, \frac{2n+1}{2^n n!}x^{2n})
La primitive F de f qui s'annule en 0 vaut:
=\sum_{n \geq 0} {(-1)}^n \frac{x^{2n+1}}{2^n n!}=xe^{ \frac{ - x^2}{2}})
conclusion: L'équation admet une solution
)
En intégrant par partie dans (E1),
du= x \int_{0}^{x} \, f(t)dt - \int_{0}^{x} \int_{0}^{a} \, f(t)dtda)
on voit que le problème (E1),avec les conditions initiales imposées, est un problème de Cauchy, il admet donc une solution maximale et une seule.
remarque: Le résultat suggère une autre piste de démonstration:
chercher un facteur intégrant de (E2) sous la forme})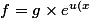
Cordialement,
La démonstration est assez longue,désolé.
en faisant le changement de variable u=x-t, on trouve:
on en déduit que f est indéfiniment dérivable et f(0)=1.
En dérivant l'égalité E1, on obtient:
d'où f'(0)=0.
En dérivant l'égalité (E2), on montre par récurrence sur l'entier n que:
soit
d'où
En écrivant f comme somme de sa série de Taylor en l'origine:
La primitive F de f qui s'annule en 0 vaut:
conclusion: L'équation admet une solution
En intégrant par partie dans (E1),
on voit que le problème (E1),avec les conditions initiales imposées, est un problème de Cauchy, il admet donc une solution maximale et une seule.
remarque: Le résultat suggère une autre piste de démonstration:
chercher un facteur intégrant de (E2) sous la forme
Cordialement,
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :