Nature d'intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
blowcoxx
- Membre Naturel
- Messages: 26
- Enregistré le: 01 Oct 2007, 21:38
-
 par blowcoxx » 18 Déc 2007, 18:16
par blowcoxx » 18 Déc 2007, 18:16
Bonsoir, je viens d'avoir un Exam en analyse et je voudrais savoir quel est la nature des intégrales suivants, pour voir si je peux quand même espérer avoir quelques points...
1)
}{t}dt)
2)
}{sqrt{1+t}}dt)
3)
 dt)
4)
dt)
Aussi il était demander de calculer la limite en
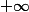
de
^{\frac{1}{3}}-x)
en utilisant les développements limités. Je vois pas comment faire !! Vous trouvez quoi?
-
BQss
- Membre Irrationnel
- Messages: 1202
- Enregistré le: 02 Nov 2006, 03:32
-
 par BQss » 18 Déc 2007, 19:15
par BQss » 18 Déc 2007, 19:15
salut,
1)converge: en 0 equivalent à 1/x^(1/2)
2)converge: chercher a majorer la valeur absolue de l'integrale par une suite covergente
3) diverge: prendre la limite en l'infini de l'integrale de 0 à n
4)converge: en +l'inf equivalent a 1/x^2 et en 0 negligeable devant 1/x^(1/2)
-
BQss
- Membre Irrationnel
- Messages: 1202
- Enregistré le: 02 Nov 2006, 03:32
-
 par BQss » 19 Déc 2007, 09:34
par BQss » 19 Déc 2007, 09:34
Et pour le dl, puisque apparemment c'est desert je m'y colle ;),
il suffit de factoriser par x^3 :
(x^3(1/x+7/x^3+1))^1/3-x=x(1+u)^(1/3)-x et d'appliquer le dl (à l'ordre 1 ca suffit) a (1+u)^(1/3) en 0, ce qui donne au final x+1/3-x+o(1/x)=1/3 en l'infini. Et la limite vaut donc 1/3.
-
BQss
- Membre Irrationnel
- Messages: 1202
- Enregistré le: 02 Nov 2006, 03:32
-
 par BQss » 19 Déc 2007, 10:09
par BQss » 19 Déc 2007, 10:09
Pour la 2 ca mérite peut-etre de devellopper:
|
}{(1+t)^{1/2}} dt)
| a la meme nature que |
}{t^{1/2}} dt|)
=
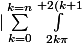\Pi} \,\,\frac{cos(t)}{t^{1/2}} dt\,+\,\int_{2(k+1)\pi}^{+\infty} \frac{cos(t)}{t^{1/2}} dt|)
donc
}{t^{1/2}} dt|\,\leq\,|\sum_{k=0}^{k=n} \int_{2k\pi}^{+2(k+1)\Pi} \,\,\frac{cos(t)}{t^{1/2}} dt|\,+\,\int_{2(k+1)\pi}^{+\infty} \frac{1}{t^{1/2}} dt)
et donc la on pourrait facilement conclure a la convergence avec une puissance supérieur à 1, mais avec 1/2 on peut pas conclure a la convergence avec ce genre de minoration... Je laisse ca a qui veut poursuivre.
*edit:Ok il faut utiliser directement une égalité et tomber sur une série convergente car l'intégrale n'est pas absolument convergente (on voit qu'on aura il me semble une somme du type

avec epsilon qui tend vers 0 suffisamment vite), si quelqu'un veut le faire et le formaliser moi j'y vais j'ai du taff...
 par busard_des_roseaux » 19 Déc 2007, 14:43
par busard_des_roseaux » 19 Déc 2007, 14:43
BQss a écrit:3) diverge: prendre la limite en l'infini de l'integrale de 0 à n
bien non. c'est faux.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 19 Déc 2007, 16:17
par Pythales » 19 Déc 2007, 16:17
C'est même une intégrale de Fresnel, dont on connaît la valeur exacte.
-
BQss
- Membre Irrationnel
- Messages: 1202
- Enregistré le: 02 Nov 2006, 03:32
-
 par BQss » 19 Déc 2007, 17:09
par BQss » 19 Déc 2007, 17:09
ah bon surement alors je l'ai pas calculé et je suspectais qu'en linéarisant puis integrant de [0,n] on verrait tendre ca vers l'infini.
Calculons le pour verifier:
} 2 dx=[x/2-sin(2x)/4]_0^n=n/2-sin(2n))
qui tend vers l'infini en l'infin donc je suis sceptique
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 19 Déc 2007, 17:12
par Nightmare » 19 Déc 2007, 17:12
Bonjour :happy3:
Erratum BQss, l'intégrande et sin(t²) et non sin²(t)
:happy3:
-
BQss
- Membre Irrationnel
- Messages: 1202
- Enregistré le: 02 Nov 2006, 03:32
-
 par BQss » 19 Déc 2007, 17:16
par BQss » 19 Déc 2007, 17:16
Nightmare a écrit:Bonjour :happy3:
Erratum BQss, l'intégrande et sin(t²) et non sin²(t)
:happy3:
oula oui lol, j'avais lu sin^2(t). sin(t^2) a toute les raisons du monde de converger en effet

, sin^2 j'en doutais fort

.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 19 Déc 2007, 17:27
par yos » 19 Déc 2007, 17:27
Pour la 2, deux IPP.
Idem pour 3, mais u=t² avant.
La 4 cv mais en 0, il faut une primitive"
-
BQss
- Membre Irrationnel
- Messages: 1202
- Enregistré le: 02 Nov 2006, 03:32
-
 par BQss » 19 Déc 2007, 17:37
par BQss » 19 Déc 2007, 17:37
yos a écrit:La 4 cv mais en 0, il faut une primitive"
en 0 ca converge car negligeable devant

, que veux tu dire en parlant de la primitive? Il n'est pas necessaire d'intégrer,
/X^{1/2})
tend vers 0 en l'infini... Et

est integrable sur ]0,1]
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 19 Déc 2007, 19:00
par yos » 19 Déc 2007, 19:00
Ah oui ça marche aussi.
Je disais ln(1+1/t²) équivalent à -2lnt (primitive 2t-2tlnt).
-
BQss
- Membre Irrationnel
- Messages: 1202
- Enregistré le: 02 Nov 2006, 03:32
-
 par BQss » 19 Déc 2007, 19:08
par BQss » 19 Déc 2007, 19:08
ah ok je vois.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités