Bonjour à tous ! Alors j'ai un DM qui se compose en 2 parties : 1) Méthode géométrique et 2)Utilisation des nombres complexes
J'ai réussi à faire toute la 1ère partie et je bloque sur la 2ème partie !
Voilà, si vous voulez bien m'aider à avancer...
Le but de l'exercice est de montrer que la droite (AD) et une hauteur du triangle ABC et que AD = BC.
2. Utilisation des nombres complexes
Le plan est muni d'un repère orthonormal direct. On désigne par a, b et c les affixes respectives des points B et C.
a. Calculer les affixes des points S et M en fonction de b et c. (sachant que moi j'appelle s l'affixe de S et m celle de M)
b. Calculer l'affixe du vecteur AD et celle du vecteur BC. En déduire que ces 2 vecteurs sont orthogonaux et que AD = BC.
Voilà la figure :
http://img156.imageshack.us/my.php?image=sanstitrekt6.jpg
TS - Nombres complexes et rotations
3 messages
- Page 1 sur 1
par tize » 14 Déc 2007, 23:57
Bonjour,
d'après ce que j'ai vu :
le vecteur AM est obtenu à partir de AB par une rotation d'angle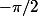
donc : e^{-i\pi/2})
de même e^{i\pi/2})
de plus (en vecteur) AD=AM+MD=AM+AS donc l'affixe de AD est e^{-i\pi/2}+ (c-a)e^{i\pi/2})
or BC=BA+AC donc d'affixe : +(c-a)=(b-a)e^{-i\pi}+(c-a))
et on s'aperçoit alors que l'affixe de BC est égale à celle de AD multipliée par 
, autrement dit BC est obtenue par la rotation de AD d'un angle de 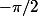c'est pourquoi ils sont orthogonaux...
d'après ce que j'ai vu :
le vecteur AM est obtenu à partir de AB par une rotation d'angle
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :