Limite de fonction

par **pedro333** » 10 Déc 2007, 13:31

bonjour,
help me

limite quand x tend vers +oo

(n^2-rac carrée(n^4-7))/(6n^2-rac carrée(36n^4-1))

par **raito123** » 10 Déc 2007, 13:54

Bonjours,

=

.
mtn tu peux multiplier par les conjugués, mais tu peux sans poser tout cela multiplier par les conjugués depuis le début c'est moins long.

par **pedro333** » 10 Déc 2007, 16:45

ben moi j'ai fait le conjugué des le debut:

(n^4-n^4 - 7)/( (6n^2-rac(36n^4-1)*(n^2+rac(n^4-7))
et je trouve :

-7/((6n^2-rac(36n^4-1)*(n^2+rac(n^4-7))

et je ne sais pas comment simplifié le denominateur!
merci de m'aider

par **Nightmare** » 10 Déc 2007, 16:56

Bonjour,

à coup de développement limité ça se règle très bien.

par **raito123** » 10 Déc 2007, 17:45

La multiplication par les conjugués dés le debut donne:

=

par **poupou9889** » 10 Déc 2007, 17:54

Ok c'est bon je trouve la même chose pour la première étape mais apres ta factorisation par 42n² je suis pas sur du coup kelkun oré une calculette graphique pour vérifier que ca tend vers 42 kar rac (36n^4-1) je pense pas kon é le droit de dire ke c'est égal à 6n² - 1 voila est ce ke tu peux expliké ta methode stp

par **raito123** » 10 Déc 2007, 18:16

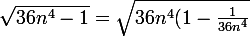et on sait que

est positive alors

donc on a

puis j'ai factoriser et j'ai multiplier 6 fois 7 qui donne 42 à moins que j'ai oublier la table de multiplication.

par **poupou9889** » 10 Déc 2007, 18:18

ok merci du détail j'avais pas vu la factorisation sous la racine non t'as pas oublié tes tables de multiplication lol merci de ton aide bye a+

par **pedro333** » 11 Déc 2007, 11:01

la reponse est bien 42 en +oo!
merci a tous

par **raito123** » 11 Déc 2007, 12:31

Ah bon tu me corrige mtn!

Limite de fonction

limite de fonction

Qui est en ligne