Petit exo sur la diagonalisation

par **pouik** » 08 Déc 2007, 16:37

Bonjour,
Pourriez vous m'aider à resoudre ce petit exercice car j'ai un peu de difficultés sur quelques questions. Merci d'avance pour votre aide.

Soit

une matrice vérifiant la relation

.
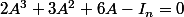
1. Montrer que A est inversible.
2. Montrer que A est diagonalisable sur

.
3. Montrer que det

.

par **pouik** » 08 Déc 2007, 16:42

Pour la 1.

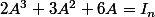
donc :

donc

est inversible d'inverse :

Pour la 2.
le polynôme annulateur de

est

,
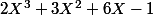
et sur

ce polynôme est scindé d'après le Théorème de d'Alembert-Gauss. Il manque juste à montrer que les racines sont simples et on pourra en déduire que

est diagonalisable sur

mais je ne vois pas comment faire.

Pour la 3.
Je ne vois pas comment faire;

par **ThSQ** » 08 Déc 2007, 16:45

K= IR sinon c'est faux non ?

Pour 2 regarde le polynome dérivé

Pour 3, la racine réelle est > 0 et les 2 cxes sont conjugués

par **pouik** » 08 Déc 2007, 17:01

Désolé mais je ne comprends pase ce que signifie cette remarque

ThSQ a écrit:K= IR sinon c'est faux non ?

et pour :

ThSQ a écrit:Pour 2 regarde le polynome dérivé

le polynôme dérivé est

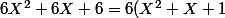qui admet deux racines complexes conjuguées qui sont :

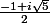
et

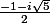
mais que dois-je faire avec ceci ??

par **pouik** » 08 Déc 2007, 17:42

désolé mais je ne comprends pas : les déterminants sur C n'existent pas ? c'est bien ca ? Pourquoi ? Je ne suis d'accord qu'il n'y a pas d'ordre sur le corps C, mais je ne vois pas bien le rapport !!

Sinon pour le polynôme dérivé, je ne vois pas comment l'utiliser... :cry:

par **SimonB** » 08 Déc 2007, 17:54

pouik a écrit:désolé mais je ne comprends pas : les déterminants sur C n'existent pas ? c'est bien ca ? Pourquoi ? Je ne suis d'accord qu'il n'y a pas d'ordre sur le corps C, mais je ne vois pas bien le rapport !!

Comment un nombre complexe pourrait-il être positif ?

par **pouik** » 08 Déc 2007, 18:26

oui mais avec des nombres complexes conjugués en faisant le produit on obtient des réels...

a moins que je ne me trompe ? :hum:

par **pouik** » 08 Déc 2007, 18:49

Rain' a écrit:qu'est ce qui te dit que la dimension du sous espace propre est la même pour chacune des racines complexes conjuguées ?

rien apparament.

Donc si je dois conclure pas de déterminant sur C ! c'est bien ca ?

Sinon pour le polynôme dérivé, à quoi sert - il ?

par **tize** » 08 Déc 2007, 19:01

pouik a écrit:...Donc si je dois conclure pas de déterminant sur C ! c'est bien ca ?...

Non, on peut tout à fait définir le déterminant sur

ou sur n'importe quel anneau commutatif, il ne faut pas exagérer quand même...
disons que la question devrait plutôt être montrer que det

est réel et ensuite det

par **ThSQ** » 08 Déc 2007, 19:07

pouik a écrit:Désolé mais je ne comprends pase ce que signifie cette remarque

Ben si

est une racine complexe (non réelle) du polynome alors

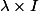
vérifie ton équation mais je vois pas comment tu vas montrer que son déterminant est > 0.

par **yos** » 08 Déc 2007, 19:17

Bonsoir.

Dans l'énoncé, il faut préciser
1) A matrice réelle
2) Montrer que A est diagonalisable sur C.

Sinon l'exo est faux.

par **pouik** » 09 Déc 2007, 16:08

Bnjour,
En fait je viens de me rendre compte que ceci est faux :

pouik a écrit:Pour la 2.
le polynôme annulateur de est ,
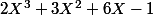
et sur ce polynôme est scindé d'après le Théorème de d'Alembert-Gauss. Il manque juste à montrer que les racines sont simples et on pourra en déduire que est diagonalisable sur mais je ne vois pas comment faire.

en fait on sait juste d'après le thm de d'alembert-Gauss qu'il y a au moins une racine sur C, mais c'est tout !
Avez vous des idées pour résoudre cette question 2. ?

Merci d'avance.

par **yos** » 09 Déc 2007, 21:31

Ca a été dit : P est un polynôme à racines simples qui annule A donc A est diagonalisable (cours).

Petit exo sur la diagonalisation

Petit exo sur la diagonalisation

Qui est en ligne