Les nombres complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
meddahi
- Messages: 7
- Enregistré le: 01 Nov 2007, 20:05
-
 par meddahi » 09 Déc 2007, 19:17
par meddahi » 09 Déc 2007, 19:17
BONSOIR:
pouvez vous m'aider à résoudre cet exercice :
j'ai un nombre complexe se trouve a la forme triangulaire je veux le traduire sous la forme algèbrique ( x+ iy)
cos

+i sin

-
SamSam
- Membre Naturel
- Messages: 40
- Enregistré le: 05 Déc 2007, 00:24
-
 par SamSam » 09 Déc 2007, 21:26
par SamSam » 09 Déc 2007, 21:26
Bonsoir,
je ne suis pas sur, mais d'apres ce que je vois, on a:
Z= cos P/11 + i sin P/11 ==> module de Z= racine de (x²+y²)= 1. (puisque Z= module de Z.(cos P/11+ i sin P/11) )
donc on a: x²+y²=1 => x= +/- y.
je ne sais plus comment continuer..
mais peut etre que tu arriveras a le résoudre suivant cette facon.
P.S: désolé pour l'ecriture non-mathematique, c'est juste que je ne sais pas ou est ce que je trouve tous les symboles =)
 par busard_des_roseaux » 09 Déc 2007, 21:28
par busard_des_roseaux » 09 Déc 2007, 21:28
meddahi a écrit:BONSOIR:
pouvez vous m'aider à résoudre cet exercice :
j'ai un nombre complexe se trouve a la forme triangulaire je veux le traduire sous la forme algèbrique ( x+ iy)
u=cos

+i sin

on a
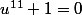
comme u

-1, u est racine de:
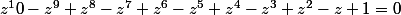
en divisant par
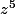
:
 -(z^4+z^{-4})+(z^3+z^{-3})-(z^2+z^{-2})+(z+z^{-1})-1=0)
on pose
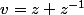
d'où:

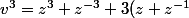)
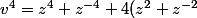+6)
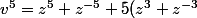+10(z^+z^{-1}))
d'où v est solution de:
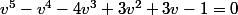
(1)
la suite prochainement...
 par busard_des_roseaux » 09 Déc 2007, 22:55
par busard_des_roseaux » 09 Déc 2007, 22:55
ensuite, je suis persuadé que l'équation (1) est résoluble par radicaux.
Il suffit de calculer des résolvantes de Lagrange pour diminuer le degré de l'équation à résoudre. Malheureusement, je n'en sais pas davantage...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
+i sin