bonjour,
petite curiosité...comment calculer le barycentre d'une arche! par exemple celui de la cardioïde (r=1+cos(teta)) ou celui d'une courbe paramétrée quelconque sur un intervalle défini ???????
merci d'avance.
aider un ptit sup ..... :triste: :triste:
Barycentre d'une arche!
18 messages
- Page 1 sur 1
par BQss » 09 Déc 2007, 15:27
Salut,
on parle d'isobarycentre d'une figure car les points ont tous la même masse si ton objet n'est que géométrique.
Ensuite tu résouds:
 dm)
avec \vec{i}+ sin(\theta) \vec{j})
est le vecteur unitaire radiale.
il faut poser :
je regarde une forme intégrable en pratique, sans garantie.
on parle d'isobarycentre d'une figure car les points ont tous la même masse si ton objet n'est que géométrique.
Ensuite tu résouds:
il faut poser :
je regarde une forme intégrable en pratique, sans garantie.
par zoé » 09 Déc 2007, 15:46
je ne voit pas comments faire aprés l'étude de la fonction en polaire (r=1+cos(teta)). integrale de (1+cos(teta))cos(teta)+(1+cos(teta)sin(teta)??? est-il possible d'avoir un exemple?
merci d'avance
merci d'avance
par BQss » 09 Déc 2007, 15:48
J'ai rajouté un dm que j'avais oublié et je regarde comment arriver a une forme eplicite.
par BQss » 09 Déc 2007, 15:55
ok j'ai trouvé je crois après faudra vérifier la validité de tous ca.
Donc comme on a dit c'est une figure geometrique, donc on recherche l'isobarycentre, i.e la densité de masse f est constante.
De plus on suppose arbitrairement que la somme des masse vaut 1 pour satisfaire a l'égalite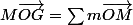
ou j'ai pris M=1.
un arc de corde élémentaire a pour longueur: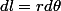
la masse élemntaire dm vaut donc:dm=f.dl=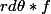
donc en intégrant de 0 à 2pi on obtient:
)d\theta=1)
avec f la constante recherchée. Soit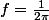 
tu remplaces f dans l'expression dm ainsi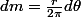
puis calcule l'intégrale, qui te donnera la coordonnée de G.
voila
Donc comme on a dit c'est une figure geometrique, donc on recherche l'isobarycentre, i.e la densité de masse f est constante.
De plus on suppose arbitrairement que la somme des masse vaut 1 pour satisfaire a l'égalite
un arc de corde élémentaire a pour longueur:
la masse élemntaire dm vaut donc:dm=f.dl=
donc en intégrant de 0 à 2pi on obtient:
tu remplaces f dans l'expression dm ainsi
voila
par BQss » 09 Déc 2007, 16:05
zoé a écrit:=
(1+cos(\theta))\vec{i}+ sin(\theta)(1+cos(\theta)) \vec{j} ]dm)
je trouve que ton intégrale = 0 il y a un probleme non???
La tu ne peux pas intégrer qui dépend de m?
non regarde le post au dessus il faut exprimer dm en fonction de theta.
Je te montre ce que j'obtiens, et après je me taillos
par BQss » 09 Déc 2007, 16:12
ca donne donc:
=(1+cos(\theta))\vec{i}+ sin(\theta)(1+cos(\theta)) \vec{j} ].(\frac{r}{2\pi})d\theta)
remplace le r par son expression en fonction de theta :
=(1+cos(\theta))\vec{i}+ sin(\theta)(1+cos(\theta)) \vec{j} ].(\frac{1+cos(\theta)}{2\pi})d\theta)
finalement voila ta forme explicite:
(1+cos(\theta))(\frac{1+cos(\theta)}{2 \pi})d\theta\,\, \vec{i}\,\,+\,\, \int_0^{2 \pi} sin(\theta)(1+cos(\theta)) .(\frac{1+cos(\theta)}{2 \pi})d\theta \,\, \vec{j})
et on intègre
.
remplace le r par son expression en fonction de theta :
finalement voila ta forme explicite:
et on intègre
.par BQss » 09 Déc 2007, 16:25
PS: pour intégrer ca tu linéarises les cos^2, cos^3, sin^2, sin^3 biensur...
Ce serait cool que tu me dises combien tu trouves pour l'intégrale et si la position de l'isobarycentre sur un graphique est cohérente, je crois que c'est bon.
Ce serait cool que tu me dises combien tu trouves pour l'intégrale et si la position de l'isobarycentre sur un graphique est cohérente, je crois que c'est bon.
par BQss » 09 Déc 2007, 16:49
Si tout se passe bien, tu vas trouver la coordonnée en j nulle, car vu la symétrie de la figure, le centre de gravité est sur l'axe des Oi.
* edit:euh non.
bon je trouve:
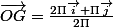
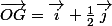
la coordonnée i au vu du dessein semble juste par contre j'aurais voulu 0 en j.
Je reverrai ca a un autre moment.
*edit correction
les intégrales donne bien:
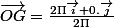
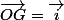
* edit:euh non.
bon je trouve:
la coordonnée i au vu du dessein semble juste par contre j'aurais voulu 0 en j.
Je reverrai ca a un autre moment.
*edit correction
les intégrales donne bien:
par nuage » 09 Déc 2007, 21:31
Salut,
en utilisant Mathematica, je suis un peu paresseux ce soir, je trouve :
Ce qui semble assez vraisemblable.
A+
en utilisant Mathematica, je suis un peu paresseux ce soir, je trouve :
Ce qui semble assez vraisemblable.
A+
par BQss » 09 Déc 2007, 23:02
Ok merci nuage, c'est ce que je pensais reste a voir pourquoi en j ca s'annule pas comme prévu.
par BQss » 09 Déc 2007, 23:28
Ok, j'ai revérifié l'integrale pour la coordonnée j vaut bien 0, un petit signe oublié qui avait changé le résultat.
Bon c'est cool, le barycentre vaut donc bien
comme prévu et les intégrales sont exactes.
Mais bon celle qui a posé la question est parti... :zen:
Bon c'est cool, le barycentre vaut donc bien
Mais bon celle qui a posé la question est parti... :zen:
par zoé » 10 Déc 2007, 18:19
merci pour vos reponse , en effet après avoir moi mëme fait le cacul je trouve les bonnes coordonnées mé est-il possible d'avoir une explication je ne comprend pas le début?comment généraliser pour les courbes paramétré telle que la cycloide, cissoide...???
merci davance
merci davance
par BQss » 10 Déc 2007, 18:59
Salut, la formule génerale valable pour n'importe quoi, serait alors:
avec P=périmètre,
)
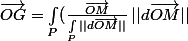le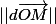
dans le plan c'est un dl, si tu as le rayon il vaut 
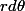par exemple, pour l'axe Oi il vaut dx etc... Ensuite 
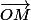se paramètre à l'aide de la variable d'intégration et d'un repère fixe associé de préférence.
quand tu a les coordonnées x et y en paramétrique, tu peux aussi exprimer x en fonction de y ou y en fonction de x, plutot que d'intégrer par rapport a ce paramètre si c'est plus facile(exemple à la place de
):
par exemple y=f(x), dy=f'(x)dx et donc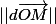=^2)^{1/2}dx)
et en intégrant ca donne:
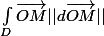= ^2)^{1/2}dx\,\vec{i} + \int_Df(x)(1+f'(x)^2)^{1/2}dx\,\vec{j})
normé par le périmètre.
ou on intègre sur les différents domaine D ou y est fonction de x et ont fait la somme sur tous les domaines.
Biensur si tu as le rayon en fonction de l'angle ca donne:
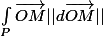= ^2cos(\theta)d\theta\,\vec{i} + \int_Pr(\theta)^2sin(\theta)d\theta\,\vec{j})
normé par le perimètre.
avec P=périmètre,
le
quand tu a les coordonnées x et y en paramétrique, tu peux aussi exprimer x en fonction de y ou y en fonction de x, plutot que d'intégrer par rapport a ce paramètre si c'est plus facile(exemple à la place de
par exemple y=f(x), dy=f'(x)dx et donc
normé par le périmètre.
ou on intègre sur les différents domaine D ou y est fonction de x et ont fait la somme sur tous les domaines.
Biensur si tu as le rayon en fonction de l'angle ca donne:
normé par le perimètre.
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :