Prise de tete exponentielle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
skysurf3000
- Membre Naturel
- Messages: 17
- Enregistré le: 15 Nov 2007, 16:59
-
 par skysurf3000 » 07 Déc 2007, 23:27
par skysurf3000 » 07 Déc 2007, 23:27
Soit l'equation:
(

)

avec n>=3
On montre facilement que (

) admet touvours 2 solutions
Les racines inférieurs forment la suite
)
Les racines supérieures forment la suite

Donner les expressions des 2 suites...
Bon courage
PS:je suis qu'en TS et ce probleme na rien d'urgent donc allez pas trop vite dans vos réponses SVP!!
-
skysurf3000
- Membre Naturel
- Messages: 17
- Enregistré le: 15 Nov 2007, 16:59
-
 par skysurf3000 » 08 Déc 2007, 14:56
par skysurf3000 » 08 Déc 2007, 14:56
pour ceux que ca intéresse j'ai peut etre une piste:
n=
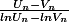
Mais je sais pas trop quoi en tirer...
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 08 Déc 2007, 15:15
par tize » 08 Déc 2007, 15:15
Bonjour,
qu'entends tu par "les équations des 2 suites..." ??
-
skysurf3000
- Membre Naturel
- Messages: 17
- Enregistré le: 15 Nov 2007, 16:59
-
 par skysurf3000 » 08 Déc 2007, 16:38
par skysurf3000 » 08 Déc 2007, 16:38
lol dsl je voulais dire "donner l expression de
)
et
)
"...
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 08 Déc 2007, 16:43
par tize » 08 Déc 2007, 16:43
Si tu cherches à exprimer ces suites en fonctions de n, je ne pense pas que cela soit possible...par contre on peut néanmoins chercher d'autres informations du genre croissance/décroissance, limites ...
-
skysurf3000
- Membre Naturel
- Messages: 17
- Enregistré le: 15 Nov 2007, 16:59
-
 par skysurf3000 » 08 Déc 2007, 16:50
par skysurf3000 » 08 Déc 2007, 16:50
je t'avouerai que le prof m'a plus balancé ça comme ça a la fin d'un cours que comme un truc bien mis en forme, type DM.
Donc effectivement, si ça se trouveil faut juste voire à quoi elles ressemblent mais a mon avis on peut arriver a les exprimer, au moins en fonction du (des) terme(s) d'avant...
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 08 Déc 2007, 16:53
par ThSQ » 08 Déc 2007, 16:53
skysurf3000 a écrit:a mon avis on peut arriver a les exprimer, au moins en fonction du (des) terme(s) d'avant...
A mon avis on peut pas non plus les exprimer et ça empêche pas de dire des tas de trucs super intéressants dessus !
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 08 Déc 2007, 17:30
par xyz1975 » 08 Déc 2007, 17:30
Bonjour,
Il est impossible d'expliciter les solutions.
-
skysurf3000
- Membre Naturel
- Messages: 17
- Enregistré le: 15 Nov 2007, 16:59
-
 par skysurf3000 » 08 Déc 2007, 17:36
par skysurf3000 » 08 Déc 2007, 17:36
xyz1975 a écrit:Bonjour,
Il est impossible d'expliciter les solutions.
Eux ben moi je vous crois, mais j'aimerai bien que tu m'expliques ce qui te permette d'etre si catégorique, et je veux bien de l'aide pour
ThSQ a écrit:dire des tas de trucs super intéressants dessus !
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 08 Déc 2007, 18:41
par yos » 08 Déc 2007, 18:41
skysurf3000 a écrit:Soit l'equation:
(

)

avec n>=3
On montre facilement que (

) admet touvours 2 solutions
Je dirais 3 solutions si n est pair.
-
skysurf3000
- Membre Naturel
- Messages: 17
- Enregistré le: 15 Nov 2007, 16:59
-
 par skysurf3000 » 08 Déc 2007, 18:52
par skysurf3000 » 08 Déc 2007, 18:52
Ah oui, ta raison, j'avais commencé a travailler que sur [0;+oo[ pour pouvoir utiliser le logaritme
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 08 Déc 2007, 19:07
par yos » 08 Déc 2007, 19:07
Donc on travaille sur R+.
Soit
=\frac{\ln x}{x})
. On a
=f(v_n)=\frac{1}{n})
, et les variations de f montrent alors que

.
De plus
)
tend vers 0, donc

tend vers 1 et

tend vers

.
Et aussi :
)
décroit donc
)
décroit.
)
décroit donc
)
croit.
Pour une formule explicite je confirme que c'est pas la peine.
-
skysurf3000
- Membre Naturel
- Messages: 17
- Enregistré le: 15 Nov 2007, 16:59
-
 par skysurf3000 » 08 Déc 2007, 20:59
par skysurf3000 » 08 Déc 2007, 20:59
Merci beaucoup, j'ai fini par comprendre ce que tu avais fait sans trop m'arracher les cheveux :we:
j'avais bien réussi a voir un raport avec ta fonction
(ou plutot son inverse) mais sans réussire à en tirer quoi que ce soit...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités