Diagonalisation et changement de base
17 messages
- Page 1 sur 1
Diagonalisation et changement de base
Bonjour à tous,
voici un exercice que je n'arrive pas à résoudre entièrement:
On considère la matrice réelle
A= 2 1 0 appartenant à M3(IR).
1 2 0
0 0 3
1) Déterminer le polynôme caractéristique PA de la matrice A.En déduire que les valeurs propres de A sont 1 et 3.
2)Déterminer les sous-espaces propres de A (on donnera une base B1 de E1 et une base B3 de E3).En déduire que A est diagonalisable.
3) Montrer que la famille B=B1 U B3 est une base de IR(3)
Je bloque sur cette troisième question.
Pour la question 2) j'ai trouvé pour E1 : vect{(1 -1 0)} et pour E3 : vect{(1 1 0)} peut-être me suis-je trompé?
Est-ce que ces résultats sont justes? Comment dois-je procéder pour le 3)?
Merci beaucoup pour votre aide!!! :we:
voici un exercice que je n'arrive pas à résoudre entièrement:
On considère la matrice réelle
A= 2 1 0 appartenant à M3(IR).
1 2 0
0 0 3
1) Déterminer le polynôme caractéristique PA de la matrice A.En déduire que les valeurs propres de A sont 1 et 3.
2)Déterminer les sous-espaces propres de A (on donnera une base B1 de E1 et une base B3 de E3).En déduire que A est diagonalisable.
3) Montrer que la famille B=B1 U B3 est une base de IR(3)
Je bloque sur cette troisième question.
Pour la question 2) j'ai trouvé pour E1 : vect{(1 -1 0)} et pour E3 : vect{(1 1 0)} peut-être me suis-je trompé?
Est-ce que ces résultats sont justes? Comment dois-je procéder pour le 3)?
Merci beaucoup pour votre aide!!! :we:
re
Salut pour E1, je trouve comme toi: vect (1;-1;0) mais pour E3
je trouve vect{(1,1,0);(1,1,1)}
On a bien = E1
= E1 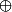 E3
E3
je trouve vect{(1,1,0);(1,1,1)}
On a bien
re
Salut pour E1, je trouve comme toi: vect (1;-1;0) mais pour E3
je trouve vect{(1,1,0);(1,1,1)}
On a bien = E1
= E1 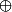 E3
E3
je trouve vect{(1,1,0);(1,1,1)}
On a bien
re
Non , pas tout à fait, je trouve x=y et z qcq !!!
donc avec X=(1,1,0) ca marche mais aussi avec X'=(1,1,1) !!!
donc avec X=(1,1,0) ca marche mais aussi avec X'=(1,1,1) !!!
attends..
on est bien d'accord que le polynome caracteristique qu'on obtient est egal a:
(3-x)(x^2-4x+4)? (puisque P=det(A-gamma*I) ) , gamma=x.
donc on a bien x1= 3 et x=2 (apres avoir calculer le discriminant delta=0)..
corrige moi si j'ai tort s'il te plait; pourtant j'ai refait l'exercice plus qu'une fois et j'ai toujours obtenu 2 et pas 1..
on est bien d'accord que le polynome caracteristique qu'on obtient est egal a:
(3-x)(x^2-4x+4)? (puisque P=det(A-gamma*I) ) , gamma=x.
donc on a bien x1= 3 et x=2 (apres avoir calculer le discriminant delta=0)..
corrige moi si j'ai tort s'il te plait; pourtant j'ai refait l'exercice plus qu'une fois et j'ai toujours obtenu 2 et pas 1..
En développant avec la dernier ligne, on a
PA(X) = (3-X)((2-X)²-1) = (3-X)(1-X)(3-X) = (3-X)²(1-X)
Et pour en revenir au problème de départ,
L'exercice nous dit clairement que A est diagonalisable, on a donc que le sous-espace propre engendré par la valeur propre 3 doit être de dimension 2.
En trouvant un seul vecteur, tu ne pouvais que te tromper.
PA(X) = (3-X)((2-X)²-1) = (3-X)(1-X)(3-X) = (3-X)²(1-X)
Et pour en revenir au problème de départ,
L'exercice nous dit clairement que A est diagonalisable, on a donc que le sous-espace propre engendré par la valeur propre 3 doit être de dimension 2.
En trouvant un seul vecteur, tu ne pouvais que te tromper.
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
