Calcul d'une limite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
chronosis
- Messages: 3
- Enregistré le: 30 Nov 2007, 13:45
-
 par chronosis » 30 Nov 2007, 14:20
par chronosis » 30 Nov 2007, 14:20
Voila j'ai un petit problème pour calculer cette limite
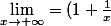^x)
Je sais qu'elle est égale à "e" ( et non egale à 1) mais je n'arrive pas à le montrer.
Tout d'abord j'ai mis que
^x)
=
})
puis j'ai posé
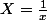
ce qui me donne
}{X}})
or je connais la limite de
}{X}})
quand X ted vers + l'infinie mais je n'arive pas à obtenir "e "à la fin.
Quelqu'un sait comment faire?
-
thedream01
- Membre Relatif
- Messages: 289
- Enregistré le: 20 Avr 2007, 10:57
-
 par thedream01 » 30 Nov 2007, 14:30
par thedream01 » 30 Nov 2007, 14:30
1/X tend vers 0 quand X tend vers l'infini...
Donc fais un DL et ça va marcher
-
BertrandR
- Membre Naturel
- Messages: 77
- Enregistré le: 25 Oct 2007, 15:13
-
 par BertrandR » 30 Nov 2007, 18:15
par BertrandR » 30 Nov 2007, 18:15
J'ajoute au cas ou : Attention à ne pas faire un DL comme si le x dans la puissance était constant !
Il faut d'abord passer au logarithme ton expression :
}{X})
avec X qui tend vers 0.
La tu fais un developpement limité du Ln qui est équivalent à X en 0 (je te laisse le faire).
Tu en déduis que
}{X})
tend vers 1 en +l'infini.
Et maintenant très important, tu ne passe pas les limites à l'exponentielledirectement, tu dis avant: Par continuite de l'exponentielle, on passe donc aux exponentielles des limites, c'est à dire
}{X})
tend vers 1
}{X}})
tend vers

Voila

-
thedream01
- Membre Relatif
- Messages: 289
- Enregistré le: 20 Avr 2007, 10:57
-
 par thedream01 » 30 Nov 2007, 18:19
par thedream01 » 30 Nov 2007, 18:19
BertrandR a écrit:J'ajoute au cas ou : Attention à ne pas faire un DL comme si le x dans la puissance était constant !
Je ne comprends pas ta remarque!
-
BertrandR
- Membre Naturel
- Messages: 77
- Enregistré le: 25 Oct 2007, 15:13
-
 par BertrandR » 30 Nov 2007, 18:22
par BertrandR » 30 Nov 2007, 18:22
Bien sur! Mais il n'existe pas de developpement limité de la fonction
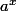
avec x variable. Enfin si il existe, mais il est impératif de repasser par l'écriture

.
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 30 Nov 2007, 18:24
par xyz1975 » 30 Nov 2007, 18:24
thedream01 a écrit:Je ne comprends pas ta remarque!
Il veut dire : il ne faut pas utiliser le DL de (1+x)^alpha pour écrire le DL de (1+x)^x car x n'est pas une constante : erreur fréquement rencontrée sur les copies des étudiants.
-
thedream01
- Membre Relatif
- Messages: 289
- Enregistré le: 20 Avr 2007, 10:57
-
 par thedream01 » 30 Nov 2007, 18:25
par thedream01 » 30 Nov 2007, 18:25
je crois que tu t'embrouilles un peu là!
Biensur que tu peux faire un DL à ln(1+1/x)!!! je ne vois pas ce qui te dérange?!
-
thedream01
- Membre Relatif
- Messages: 289
- Enregistré le: 20 Avr 2007, 10:57
-
 par thedream01 » 30 Nov 2007, 18:26
par thedream01 » 30 Nov 2007, 18:26
Ah ok! oui oui, mais moi je parlais de la formule qui a été donnée en haut, il avait déja commencé le travail!
-
The Void
- Membre Relatif
- Messages: 187
- Enregistré le: 25 Mar 2007, 20:33
-
 par The Void » 30 Nov 2007, 21:42
par The Void » 30 Nov 2007, 21:42
Salut,
Sans connaître les DL de ln, etc.. (je suis en mpsi) je pense avoir une méthode de résolution :)
ln(1+1/x) équivalent à 1/x
xln(1+1/x) équivalent à 1
=> lim xln(1+1/x) = 1
exp continue => (1+1/x)^x -> e
-
BertrandR
- Membre Naturel
- Messages: 77
- Enregistré le: 25 Oct 2007, 15:13
-
 par BertrandR » 01 Déc 2007, 00:42
par BertrandR » 01 Déc 2007, 00:42
Et dit moi, d'ou sort tu ces equivalents si tu ne connais pas les DL ? :D
 par busard_des_roseaux » 01 Déc 2007, 07:11
par busard_des_roseaux » 01 Déc 2007, 07:11
BertrandR a écrit:Et dit moi, d'ou sort tu ces equivalents si tu ne connais pas les DL ?

ces équivalents viennent du nombre dérivé du log en u=1
avec l'accroissemnt

-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 01 Déc 2007, 07:33
par lapras » 01 Déc 2007, 07:33
Bonjour,
tu ne passe pas les limites à l'exponentielledirectement, tu dis avant: Par continuite de l'exponentielle, on passe donc aux exponentielles des limites
Pourquoi est ce important de dire cette phrase ?
-
The Void
- Membre Relatif
- Messages: 187
- Enregistré le: 25 Mar 2007, 20:33
-
 par The Void » 01 Déc 2007, 09:10
par The Void » 01 Déc 2007, 09:10
BertrandR a écrit:Et dit moi, d'ou sort tu ces equivalents si tu ne connais pas les DL ?

Quand x->0, la limite de ln(x+1)/x (=ln'(x+1)=1/(x+1)) et x/x est 1 , il suffit ensuite de poser X=1/x.
-
blackpearl
- Membre Naturel
- Messages: 12
- Enregistré le: 30 Nov 2007, 13:45
-
 par blackpearl » 03 Déc 2007, 20:35
par blackpearl » 03 Déc 2007, 20:35
c'est pas +l'infini la limite de cette fonction ! enfin je pense que c sa!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités