Résolu[Forme quadratique Ev Euclidien]

[LuckyS]

Voilà j'ai un petit probleme sur un exo traitant d'une forme quadratique. J'ai eu mon cours dessus mais c'est encore un peu neuf. Voici mon pb :
on a E un Ev Euclidien de dim n muni du produit scalaire (x,y) -> , k appartenant à |R et a un vecteur de E.

Pour tout vecteur x de E, q(x) = 2*² + k||x||² .
i) Montrer que q est une forme quadratique sur E, en préciser sa forme polaire.
ii) Montrer que q est positive ssi k est supérieur ou egale à 0.
iii)Donner une CNS sur k pour que q soit définie positive.

Pour le i), je pensais montrer à partir de la definition cad, pour tout reel t, q(tx)=t²q(x) et que la forme qui a tout x,y de ExE , (q(x+y)-q(x)-q(y))/2 est bilinéaire symétrique ( qui est evident). Mon pb ici est pour la bilinéarité, je ne vois pas comment simplifier pour arriver à ce que je veux trouver.
Ensuite pour le ii) la CN est triviale.
Pour iii) Ca va normalement.

Merci de m'aider.

[tize]

Bonjour,
pour la forme polaire, je trouve 2+k; utilise le fait que et développe...
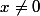
ii) prends dans l'orthogonal de

[LuckyS]

Bonjour Tize, et merci pour ton aide à mes questions,

J'ai donc pu reprendre mon calcul et en effet, en détaillant ma forme polaire je trouve bien 2 + k (Il me manquait une simplification en faite). Forme qui est belle et bien linéaire par rapport aux deux variables et qui est symétrique.
Pour mon i) c'est donc maintenant bon.
En revanche pour ii), j'ai peur de ne pas très bien saisir l'espace engendré par a, soit le Vect{a}.
Autant je peux montrer, si x est different du vecteur nul, que k doit etre supérieur ou égale à -2 par l'inégalités de Cauchy-Schwarz mais que k est supérieur à 0, je ne vois pas.
On sait aussi que a que ne peut etre un vecteur nul puisqu'il est vecteur unitaire. Pour moi, on aurait k supérieur ou égale à 0 ssi ² est nul, c'est à dire si a et x sont orthogonaux. Je n'arrive pas à aller plus loin.


Merci pour votre aide.

[tize]

Salut,
je pense que tu n'as pas compris ce que je t'ai dit :
si k est positif alors q est positive (évident)
Réciproquement (et par contraposée) si k est strictement négatif alors que vaut q(x) pour x dans l'orthogonal de Vect{a} (son signe)? Conclusion ?

[LuckyS]

Salut ,

Si k est positif ou nul, q(x) l'est aussi, et donc si q(x) est strictement négatif alors k est strictement négatif.
Ensuite je n'arrive pas très bien à en venir à la conclusion, car on montre bien que si k>=0 , q(x)>=0 , mais on ne montre pas que si q(x)>=0 alors k>=0.
Je suis désolé mais j'avoue ne pas bien voir la direction à prendre. Aussi j'ai du mal à saisir l'expression "pour x dans l'orthogonal de Vect{a}".

merci

[LuckyS]

Quelqu'un peut-il m'éclairer s'il vous plait ?

[tize]

Bonjour,
j'ai déjà répondu à ta question :
montrer que si q(x)>=0 alors k>=0 revient à montrer que si k<0 alors q n'est pas positive (c'est la contraposée !)
or si k<0 que peux tu dire du signe de q(x) pour x dans l'othogonal de Vect{a} ?

[LuckyS]

Bonjour Tize,
En effet, je suis désolé, j'ai manqué de perspicacité. Je ne sais pas pourquoi dans ma contraposé j'ai tout simple oublié de me préciser qu'il ne me suffisait qure d'un x qui verifiait avec k négatif, q(x) négatif.
Est ce que je peux te demander un indice pour la troisieme question, "Donner une CNS sur k pour que q soit positive." ?
Si q est définie, k peut etre tout reel non ? Puisque = 0 et la norme de x aussi.
Devrait-on supposer k nul ?

Merci...

[tize]

...la troisieme question, "Donner une CNS sur k pour que q soit positive."...

La 3) c'est bien "Donner une CNS sur k pour que q soit définie positive."
Déjà tu sais que k doit être supérieur ou égal à 0 sinon q n'est pas positive. Pour le côté définie, tu dois avoir q(x)=0 ==> x=0.
Déjà tu peux remarquer que si k>0 alors q(x)=0 ==> x=0
Réciproquement (et par contraposée) si k=0 alors alors que dire de q(x) pour x différent de 0 dans l'orthogonal de Vect{a}...

[LuckyS]

Un grand merci à toi Tize pour cet exercice un peu laborieux de mon coté.
Je pense avoir bien mieux saisi les notions. J'ai pu finir mon exo. Rien de vraiment méchant en fait, il faut juste bien regarder...

Merci de ton aide !