Triangle spherique

par **sarad** » 02 Déc 2007, 12:00

bonjour,
jarrive pas a resoudre un exo sur le triangle spherique : merci de m'aider.
alors on a ABC un triangle spherique non aplati. on note u= OA vectorielOB v=OA vectoriel C et w= OBvectoriel OC
1- montrer que teta = t avec teta l'angle en A du triangle et t = ecart angulaire entre u et v.
2-exprimer les autres angles de la meme maniere.
3-montrer que la somme des angles dans un triangle spherique est srictement superieure a pi.
Merci.

par **Pythales** » 02 Déc 2007, 13:07

Tu peux dire que

et

sont tous deux égaux à l'angle des plans

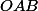
et

par **sarad** » 02 Déc 2007, 13:16

Merci bcp. donc pour les autres on trouvera la meme chose beta = ecart entre u et w avec beta l'angle en b et gama = ecart entre v et w avec gama langle en C? et svp est ce que vous sauriez comment faire la 3eme question: pour demintrer que la somme des angles est superiere a PI? Merci bcp.

par **sarad** » 02 Déc 2007, 15:02

tjrs rien?

par **busard_des_roseaux** » 02 Déc 2007, 18:30

bonsoir,
si B+C >

, il n'y a rien à démontrer.
sinon,

équivaut à:

et cette dernière inégalité se déduit de l'identité trigo:

(1)
l'identité (1) est la duale, par triangle polaire de celle bien connue:

cordialement,

par **sarad** » 02 Déc 2007, 18:41

merci bcp pour la reponse,
je devrais repondre a la question en utilisant les questions qui precedent et en utilisant des vecteurs et le determinant je pens :s.

par **busard_des_roseaux** » 02 Déc 2007, 18:55

oui, on utilise aussi le produit mixte.

Triangle spherique

triangle spherique

Qui est en ligne