Aires et barycentre

[Jacky]

Bonjour je suis bloqué sur les questions suivantes :
On considère le triangle ABC. M est un point de [BC] distinct de B et de C

1) Montrer que M est le barycentre de (B;MC);(C;MB)
Ma réponse est :
Soit [BC] = a
On sait que M appartient à [BC], on en déduit la longueur de [BM]
BM=xa
Par suite : on en déduit [MC]
MC = BC-BM = a-xa = (1-x)a
Par suite on a M barycentre de (B;xa) (C;((1-x)a)
avec xa + (a-xa) = a (a différent de 0 )

2) En déduire que M est aussi le barycentre de (B;aire (AMC)) et (C;aire (AMB))
Mon idée est de refaire un peu comme dans la première question mais j'ai l'impression qu'il y a quelque chose qui ne va pas.
Soit [AM] = ya
AMC= (AM x MC)/2= (ya (1-x)a)/2=(ya² -xya²)/2
AMB= (AM x MB)/2=[(ya) ( xa)]/2=[(xy)a]/2
Par suite M est le barycentre de (B;((ya²-xya²)/2) (C;([(xy)a]/2)
avec (ya² -xya²)/2 + [(xy)a]/2 différent de 0
Merci de vos réponses

[hellow3]

Bonjour je suis bloqué sur les questions suivantes :
On considère le triangle ABC. M est un point de [BC] distinct de B et de C

1) Montrer que M est le barycentre de (B;MC);(C;MB)
Ma réponse est :
Soit [BC] = a
On sait que M appartient à [BC], on en déduit la longueur de [BM]
BM=xa
Par suite : on en déduit [MC]
MC = BC-BM = a-xa = (1-x)a
Par suite on a M barycentre de (B;xa) (C;((1-x)a)
avec xa + (a-xa) = a (a différent de 0 )
Ce qu'on veut c'est M=Bar{(B,(1-x)a); (C;ax)}
Et faut le montrer. (1-x)a MB + ax MC = 0 (en vecteurs)
C'es tplus simple si tu remarques:
Soit un vecteur unitaire , de même direction et sens que
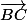
alors,
alors,
alors,
donc
Donc M=Bar{(B,MC)(C,MB)}

2) En déduire que M est aussi le barycentre de (B;aire (AMC)) et (C;aire (AMB))
Mon idée est de refaire un peu comme dans la première question mais j'ai l'impression qu'il y a quelque chose qui ne va pas.
Oui. AM n'est pas la hauteur, appelle la AH plutôt.
Soit [AM] = ya
AMC= (AM x MC)/2= (ya (1-x)a)/2=(ya² -xya²)/2
AMB= (AM x MB)/2=[(ya) ( xa)]/2=[(xy)a]/2
Par suite M est le barycentre de (B;((ya²-xya²)/2) (C;([(xy)a]/2)
avec (ya² -xya²)/2 + [(xy)a]/2 différent de 0

Pars de:


tu dois arriver à:


Merci de vos réponses

Le principe était bon.