Calcul de primitive

[shawn12]

Bonjour a tous, je dois calculer des primitives mais je ne sais pas comment m'y prendre, pouvez-vous m'aider ?

Les primitives à trouver sont celles des fonctions suivantes :


et


de quelle forme de primitive dois-je me servir : u'/u -> ln(u) ?

[cesson]

mets x^2+x+1 sous forme canonique donc (x+1/2)^2+3/4 soit de la forme x^2+u^2 qui aura donc une primite du type Arctg

[B_J]

Salut;
commence par ecrire le denominateur sous forme canonique

[fatal_error]

Bonjour, concernant la première,
1/(x²+x+1).
Généralement : on décompose la fraction rationnelle. Les termes dont le dénominateur est x, on y va a coup de ln. Les termes dont le dénominateur est en x², on y va a l'arctan. (c'est une méthode qui marche).

Donc pour la première, on veut faire apparaitre une fraction de la forme C/1+y² dont la primitive est Carctan(y).
on veut x²+x+1=C(1+y²) avec un changement de variable adéquat.
x²+x+1=(x+1/2)²+3/4=3/4*([sqrt(4/3)*(x+1/2)]²+1)
Il ne reste plus qu'a changer de variable en posant y='lexpression entre crochets'.

Pour la seconde, fraction rationelle, pis même procédé.

[shawn12]

merci pour vos réponses rapides mais je ne comprend pas comment fatal_error passe de



à

[B_J]

[shawn12]

Comment dois-je procéder pour le changement de variable ?

Je pose
?

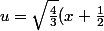Mais ensuite ???

La primitive de n'est elle pas simplement ? Puisque je ne recherche que la primitive et pas l'intégrale...

[shawn12]

En ce qui concerne la deuxième fraction, je ne vois pas comment traiter le x+1 du numérateur. Cela ne correspond à aucune primitvé évidente...

Est-ce que quelqu'un pourrait m'indiquer comment m'y prendre ?

[fatal_error]

Pour la seconde, decompose ta fraction en élément simple...
Concernant la première, si tu fais l'intégrale de 0 à x de f(t)dt, tu obtiens une primitive F(x) de f(x) à une constante près(F(0)). Il ne te reste qu'a changer tes bornes d'intégration (seule la supérieur est importante). ps : le du est correct