Encore les séries....Dzeta de Riemann

[bilou88]

on note Dzeta(x) la série de terme général 1/n^x, son ensemble de défition est x appartiennent a ]1,+inf[.On me demande de montrer que lim(x tend vers 1) de Dzeta(x)=+inf, en comparant avec une intégrale...Je ne vois pas du tout comment partir.Pouvez vous m'aider?merci d'avance

[kazeriahm]

salut

est-ce que tu as vu le théorème de comparaison d'une série et d'une intégrale ?

on peut le rencontrer sous plusieurs noms mais il te dit que selon certaines hypothèses sur une fonction f,

la série de terme générale f(n) et l'intégrale de f entre a et l'infini ont meme nature (avec a arbitraire)

[bilou88]

je n'ai pas encore fait d'exemple d'application de ce théorème, j'aurai besoin de voir comment on fait..

[kazeriahm]

bien donc tu prend un x fixé dans ]1,l'infini[

tu considère la fonction f:t->1/t^x

Tu montres que f est continue est décroissante sur [1,+l'infini[

Regarde bien que x est fixé et que ta variable est t.

Alors d'après le théorème en question, comme ta fonction f est intègrable sur [1,+l'infini[, la série des f(n) (qui vaut zeta(x)) est définie, et plus précisèment on a

[CENTER]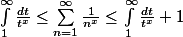[/CENTER]

Bon là tu as appliqué le théorème.

Maintenant tu peux calculer l'intégrale et regarder ce qui se passe quand x tend vers 1.