Intègrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
seham
- Membre Naturel
- Messages: 12
- Enregistré le: 21 Oct 2007, 14:13
-
-
Maeredhel
- Membre Naturel
- Messages: 26
- Enregistré le: 01 Oct 2007, 11:39
-
 par Maeredhel » 29 Nov 2007, 16:26
par Maeredhel » 29 Nov 2007, 16:26
Heu je pense que c'est plutot ln et non log, mais sinon tu peux dériver le 2eme terme et tu dois obtenir le terme dans l'intégrale ^^
-
seham
- Membre Naturel
- Messages: 12
- Enregistré le: 21 Oct 2007, 14:13
-
 par seham » 29 Nov 2007, 16:49
par seham » 29 Nov 2007, 16:49
je fait la dérivation mais j'ai pas trouver la même solution
log [ h + ( ;)² + h² ) ½ ] = ( h + ( ;)² + h² ) ½ ) / h + ( ;)² + h² ) ½
= 1+ [ ½ (;)² + h²) (;)² + h²) ] / h + ( ;)² + h² ) ½
= 1 + [ ½ .2 h (;)² + h²) ] / h + ( ;)² + h² ) ½
= 1 + h (;)² + h²) / h + ( ;)² + h² ) ½
= ???
avec ;) = cst
-
rifly01
- Membre Relatif
- Messages: 460
- Enregistré le: 30 Déc 2005, 04:38
-
 par rifly01 » 29 Nov 2007, 17:50
par rifly01 » 29 Nov 2007, 17:50
Tout simplement parce que :
=\frac{1+\frac{x}{\sqrt{x^2+a^2}}}{x+\sqrt{x^2+a^2}}=\frac{1}{\sqrt{x^2+a^2}})
-
BertrandR
- Membre Naturel
- Messages: 77
- Enregistré le: 25 Oct 2007, 15:13
-
 par BertrandR » 29 Nov 2007, 19:39
par BertrandR » 29 Nov 2007, 19:39
D'ailleurs il s'agit d'une fonction usuelle la réciproque du sinus hyperbolique, argsh(x). Tu n'a qu'a la retrouver en dérivant avec la formule
=(f'of^{-1})(x))
.
De plus la démonstration si tu veux :



donc

et enfin
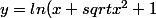)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités