équation d'une hyperbole ?
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
totor
- Membre Naturel
- Messages: 57
- Enregistré le: 24 Aoû 2005, 16:16
-
 par totor » 21 Nov 2007, 12:44
par totor » 21 Nov 2007, 12:44
bonjour,
j'aimerais savoir si l'équation :
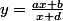
est une équation d'hyperbole ? Graphiquement je trouve une hyperbole mais dans tous les cours que je vois l'équation d'une hyperbole est définie par :
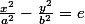
kesako ? :briques:

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 21 Nov 2007, 12:47
par raito123 » 21 Nov 2007, 12:47
La premiere est une equation d'hyperbole.juste. :++:
pour a deuxiéme je sais pas.
Les multiples ne doivent pas être utilisés sans nécessité
-
Help
- Membre Naturel
- Messages: 53
- Enregistré le: 22 Aoû 2006, 12:54
-
 par Help » 21 Nov 2007, 13:35
par Help » 21 Nov 2007, 13:35
La deuxième est l'équation générale des hyperboles. La première est un cas particulier. La première peut se mettre de la forme y=f(x) (à un x correspond un seul y). Dans la deuxième on peut avoir 2 y différents (opposés en fait) pour une même valeur de x.
-
totor
- Membre Naturel
- Messages: 57
- Enregistré le: 24 Aoû 2005, 16:16
-
 par totor » 22 Nov 2007, 13:24
par totor » 22 Nov 2007, 13:24
SAlut,
merci pour vos explications. Cependant, je ne comprend pas pourquoi dans la premiere definition il y a trois paramètres et dans la deuxième deux (si e=1 par exemple). Est-il possible d'exprimer la première définition dans la forme de la deuxième ?
merci par avance!
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 22 Nov 2007, 13:36
par Quidam » 22 Nov 2007, 13:36
totor a écrit:SAlut,
merci pour vos explications. Cependant, je ne comprend pas pourquoi dans la premiere definition il y a trois paramètres et dans la deuxième deux (si e=1 par exemple). Est-il possible d'exprimer la première définition dans la forme de la deuxième ?
merci par avance!
Non !
La première équation est celle d'une hyperbole dite "équilatère". Elle a ses asymptotes perpendiculaires, et respectivement parallèles aux axes Ox et Oy. C'est donc un cas particulier d'hyperbole. Telle qu'elle est orientée, pour chaque x différent de -d, il existe un seul point d'abscisse x !
La deuxième équation est une équation plus générale mais pas dans toute la généralité. C'est une hyperbole dont les axes de symétrie sont les axes Ox et Oy. A chaque valeur de x correspond 0 1 ou 2 points. De plus, en faisant varier les coefficients a,b,e on fait varier l'inclinaison des asymptotes ; l'angle des asymptotes n'est donc pas nécessairement un angle droit (contrairement à l'hyperbole équilatère donnée par la première équation).

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 22 Nov 2007, 13:40
par raito123 » 22 Nov 2007, 13:40
Donc avec la premiere on trouve pour chaque reel une seul image,et pas necessairement pour la deuxiéme .?
Les multiples ne doivent pas être utilisés sans nécessité
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 22 Nov 2007, 13:52
par Quidam » 22 Nov 2007, 13:52
raito123 a écrit:Donc avec la premiere on trouve pour chaque reel une seul image,et pas necessairement pour la deuxiéme .?
exact ! oui
-
totor
- Membre Naturel
- Messages: 57
- Enregistré le: 24 Aoû 2005, 16:16
-
 par totor » 22 Nov 2007, 15:11
par totor » 22 Nov 2007, 15:11
Quidam a écrit:Non !
La première équation est celle d'une hyperbole dite "équilatère". Elle a ses asymptotes perpendiculaires, et respectivement parallèles aux axes Ox et Oy. C'est donc un cas particulier d'hyperbole. Telle qu'elle est orientée, pour chaque x différent de -d, il existe un seul point d'abscisse x !
La deuxième équation est une équation plus générale mais pas dans toute la généralité. C'est une hyperbole dont les axes de symétrie sont les axes Ox et Oy. A chaque valeur de x correspond 0 1 ou 2 points. De plus, en faisant varier les coefficients a,b,e on fait varier l'inclinaison des asymptotes ; l'angle des asymptotes n'est donc pas nécessairement un angle droit (contrairement à l'hyperbole équilatère donnée par la première équation).
ok merci beaucoup pour cette explication !
dans la définition générale les paramètres a et b fonct varier l'inclinaison des asymptotes. Est ce que pour la première définition (le cas particulier) les paramètres a,b et c correspondent à une transformation en particulier ?
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 23 Nov 2007, 21:25
par Quidam » 23 Nov 2007, 21:25
totor a écrit:ok merci beaucoup pour cette explication !
dans la définition générale les paramètres a et b fonct varier l'inclinaison des asymptotes. Est ce que pour la première définition (le cas particulier) les paramètres a,b et c correspondent à une transformation en particulier ?
Je suppose ici, c et a non nuls ; je te laisse le soin de te débrouiller dans ces cas particuliers.
En outre y n'est pas défini pour x=-d/c. Quand y est défini, on peut écrire :
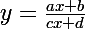
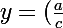\times \frac{x+\frac{b}{a}}{x+\frac{d}{c}})
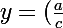\times \frac{x+\frac{d}{c}+\frac{b}{a}-\frac{d}{c}}{x+\frac{d}{c}})
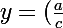\times [\frac{x+\frac{d}{c}}{x+\frac{d}{c}}+\frac{\frac{b}{a}-\frac{d}{c}}{x+\frac{d}{c}}])
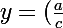\times [1+\frac{\frac{b}{a}-\frac{d}{c}}{x+\frac{d}{c}}])
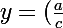+(\frac{a}{c})\times [\frac{\frac{bc-ad}{ac}}{x+\frac{d}{c}}])
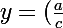+(\frac{bc-ad}{c^2})\times [\frac{1}{x+\frac{d}{c}}])
En posant
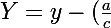)
,
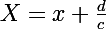
et
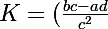)
on obtient l'équation :
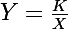
, équation d'une transformée affine de l'hyperbole 1/x !
Tu vois imméditement sous cette forme que les deux asymtotes ont respectivement pour équations :

et
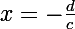
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités