Suite récurrente d'un ensemble fini
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
BiZi
- Membre Relatif
- Messages: 307
- Enregistré le: 26 Mai 2006, 21:06
-
 par BiZi » 20 Nov 2007, 18:13
par BiZi » 20 Nov 2007, 18:13
Bonjour,
J'ai un gros doute: si on prend A un ensemble fini,
}_{\in \mathbb{N})
une suite f-récurrente avec f une fonction de A dans A,
}_{\in \mathbb{N})
est-elle nécessairement périodique à partir d'un certain rang? périodique?
Merci de me répondre!
-
bruce.ml
- Membre Rationnel
- Messages: 630
- Enregistré le: 18 Juin 2007, 23:54
-
 par bruce.ml » 20 Nov 2007, 18:19
par bruce.ml » 20 Nov 2007, 18:19
Salut,
d'après le lemme des tirroirs,

. Peux-tu terminer seul ?

-
BiZi
- Membre Relatif
- Messages: 307
- Enregistré le: 26 Mai 2006, 21:06
-
 par BiZi » 20 Nov 2007, 18:56
par BiZi » 20 Nov 2007, 18:56
bruce.ml a écrit:Salut,
d'après le lemme des tirroirs,

. Peux-tu terminer seul ?

Bin c'e'st ce que je me disais: mais comme j'ai un exo où je dois montrer qu'une suite de

est périodique... Je pense que pour la périodicité il faut rajouter des conditions, non?
-
bruce.ml
- Membre Rationnel
- Messages: 630
- Enregistré le: 18 Juin 2007, 23:54
-
 par bruce.ml » 20 Nov 2007, 19:03
par bruce.ml » 20 Nov 2007, 19:03
Je ne vois pas ce qui manque, mais j'ai écrit une bêtise, la suite n'est évidemment pas forcément périodique, mais périodique à partir d'un certain rang, à partir du rang où on retombe sur une valeur déjà obtenue.

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 20 Nov 2007, 19:10
par raito123 » 20 Nov 2007, 19:10
c'est vrai que toute suite ecrite sous forme de
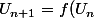)
alors

est periodique???
Les multiples ne doivent pas être utilisés sans nécessité
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 20 Nov 2007, 19:16
par ThSQ » 20 Nov 2007, 19:16
raito123 a écrit:c'est vrai que toute suite ecrite sous forme de
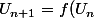)
alors

est periodique???
Si elle est à valeurs dans un ensemble fini bien sûr. Sinon pas forcément.
-
bruce.ml
- Membre Rationnel
- Messages: 630
- Enregistré le: 18 Juin 2007, 23:54
-
 par bruce.ml » 20 Nov 2007, 19:20
par bruce.ml » 20 Nov 2007, 19:20
même toute suite définie par
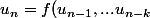)
! Toute suite recurrente d'un ensemble fini est presque périodique

-
BiZi
- Membre Relatif
- Messages: 307
- Enregistré le: 26 Mai 2006, 21:06
-
 par BiZi » 20 Nov 2007, 19:36
par BiZi » 20 Nov 2007, 19:36
ThSQ a écrit:Si elle est à valeurs dans un ensemble fini bien sûr. Sinon pas forcément.
En fait ma question c'était surtout de savoir si une telle suite est périodique ou seulement périodique à partir d'un certain rang;avec f injective en tout cas on a la périodicité, non?
-
bruce.ml
- Membre Rationnel
- Messages: 630
- Enregistré le: 18 Juin 2007, 23:54
-
 par bruce.ml » 20 Nov 2007, 19:42
par bruce.ml » 20 Nov 2007, 19:42
BiZi a écrit:En fait ma question c'était surtout de savoir si une telle suite est périodique ou seulement périodique à partir d'un certain rang;avec f injective en tout cas on a la périodicité, non?
si f est injective alors elle est surjective et bijective, c'est donc une permutation, la suite sera donc periodique de période la taille du cycle auquel 0 appartient.
Sinon en effet la suite n'est pas forcément périodique. Dans Z/2Z, tu prends la fonction f = 1, et u0 = 0, la suite vaut 0,1,1,1, ... et n'est pas périodique.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités