Terminal math Derivé

[raito123]

Bonjour,
Voici une limite qui me casse la tête :
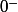
Verifier la derivabilité en de la fonction
G(x)=
bonne chance. :++:

[Skullkid]

Bonjour, la règle de l'Hospital doit marcher, je pense.

[raito123]

Bien jouer , je n'y avais pas pensé :++:

[ArthurTeddy]

Exercice interessant,

quelle est cette regle dite de l"hopital" ?

[raito123]

Pfff......
Je ne sais pas comment mais j'ai oublié un detail tout en haut
g(0)=1

[Skullkid]

ArthurTeddy : Si f et g sont deux fonctions dérivables sur ]a,b[ dont la limite en a est nulle, si g'(x) ne s'annule pas sur ]a,b[ et si alors .

Me semble qu'elle peut se généraliser un peu plus loin...enfin elle n'est pas enseignée en France, ou en tout cas on me l'a jamais enseignée, donc je ne l'ai jamais utilisée xD

raito123 tu es sûr que g(0)=1 ? Parce que si c'est le cas, g n'est pas continue en 0...

[raito123]

enfin j'ai trouvé -infini
Hey ArthurTeddy voilà ce que tu veux

[ArthurTeddy]

Merci a tous les deux ca pourrait servir dans un devoir, cette méthode métant totalement inconnue !

[Skullkid]

enfin j'ai trouvé -infini

En prenant g(0)=1 je trouve + l'infini. Tu es sûr que c'est pas plutôt g(0)=0 ?

[raito123]

bon mtn c'est claire
1/Le probléme est posé de cette façon donc cela répond a ta question.
2/La question est de verifié la derivabilité en 0 et je n'ai pas pensé à voir si g continu en 0 . En tout cas ma réponse étais que la dérivé est + infini.
Conclusion :g n'est pas dérivable à gauche de 0 ,merci Skullkid de t'avoir casser la tête avec moi lol :marteau:
Ici on fait 'hopital' mais dans un contrôle il faut la démontrer avant l'utiliser

[raito123]

En prenant g(0)=1 je trouve + l'infini. Tu es sûr que c'est pas plutôt g(0)=0 ?

ouais c'est + infini dsl :mur: