Exo dur help !!

[Anonyme]

Voici les question de l'exercice que je bute :

La suite Un est définie par la relation Un= n U (exposant n-1) + 1 avec Uo=1

1. Montrer par récurrence que l’on a Un;)2 (n !) pour n;)1.

2. On suppose qu’il existe un nombre K tel que l’on ait Un;) K (n !) pour un entier n.
Montrer que dans ces conditions on a : U(n=1) ;) K ((n+1) !).

3. Question difficile :
Montrer, en raisonnant par récurrence, que l’on a : Un < 3 (n !).
INDICATION : Si deux entiers p et q vérifient l’inégalité : p < q , alors on a p ;) q – 1.
En se servant des résultats des questions 2 et 3 , montrer qu’il n’existe pas d’entier n (exposant 0) tel que : Un(exposant 0) > 3 (n (exposant 0) !)



Voila merci de m'avancer dans les méthodes a appliquer et de m'aider car c'est pas évident !!!

[N_comme_Nul]

Salut !

Je suppose que ta suite est définie par
[CENTER]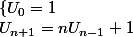[/CENTER]

1. La propriété est vérifie pour .
Si tu as alors pour avoir ta récurrence, il suffit de jeter un coup d'oeil sur la définition même de ta suite, en remarquant que et que pour tout réel,

Mais il y a un truc que je "ne capte pas", ce sont tes "exposant".

[Nicolas_75]

Probablement parce que ce sont des indices...

[N_comme_Nul]

Je me disais aussi :hum:

Bon, pour la question 3, je pense que je ferais ainsi l:

[INDENT]



[/INDENT]
()
[INDENT]
[/INDENT]()
[INDENT] [/INDENT]

[Anonyme]

Oui des indices autant pour moi. Merci beaucoup !!!!!

[Anonyme]

La question 2 vous ne l'avez pas traité ?

[N_comme_Nul]

"La question 2 vous ne l'avez pas traité ?"

Tout simplement parce que lorsque l'on sait faire la 1., on sait faire la 2. :we: