Une série numérique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
krimo
- Messages: 9
- Enregistré le: 11 Nov 2007, 16:56
-
 par krimo » 11 Nov 2007, 17:03
par krimo » 11 Nov 2007, 17:03
S1=1+1/2+1/3+...+1/n
comment calculé sa limite , je sais que c égale a 2 , mais comment le faire
et aussi comment calculé celle de :
S2=1/(1.2.3)+1/(2.3.4)+...+1/(n(n+1)(n+2))
j'ai besoin de réponse aprés demainn j'ai un devoir et j'ai bcp a faire s'il vous plait aider moi :cry:
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 11 Nov 2007, 17:44
par bitonio » 11 Nov 2007, 17:44
Non, la limite n'est pas deux. On a même

.
Au mieux, tu peux écrire que
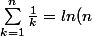+ \gamma +o(1))

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 11 Nov 2007, 17:46
par nuage » 11 Nov 2007, 17:46
Salut,
La suite S1, telle que tu l'as définie est divergente. 1+1/2+...+1/n tend vers l'infini avec n.
-
krimo
- Messages: 9
- Enregistré le: 11 Nov 2007, 16:56
-
 par krimo » 11 Nov 2007, 18:00
par krimo » 11 Nov 2007, 18:00
le développement limité on a pas encore fais , donc je préfére +l'infini mecri bcp
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 11 Nov 2007, 18:19
par ThSQ » 11 Nov 2007, 18:19
Pour S2, utlise 1/(n(n+1)(n+2) = (1/2n-1/2(n+1)) + (1/2(n+2) -1/2(n+1))
Ca fait une somme télescopique et ça fait 1/4
-
krimo
- Messages: 9
- Enregistré le: 11 Nov 2007, 16:56
-
 par krimo » 11 Nov 2007, 18:23
par krimo » 11 Nov 2007, 18:23
vous pouvez m'expliquer qu'es ce que veux dire [img];)+o(1)[/img] ( par curiosité )
-
rifly01
- Membre Relatif
- Messages: 460
- Enregistré le: 30 Déc 2005, 04:38
-
 par rifly01 » 11 Nov 2007, 18:58
par rifly01 » 11 Nov 2007, 18:58
Salut,
Si tu as fais les intégrales, les limites. Cela suffit pour prouver que la suite diverge. Pour le faire, il suffit de trouver son équivalent.
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 11 Nov 2007, 20:11
par bitonio » 11 Nov 2007, 20:11
krimo a écrit:vous pouvez m'expliquer qu'es ce que veux dire [img];)+o(1)[/img] ( par curiosité )

est le nombre d'euler et o(1) c'est "l'erreur", une quantité qui tend vers 0 (cf DL)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
