Polynome racine évidente et factorisation
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
marocain94
- Membre Relatif
- Messages: 116
- Enregistré le: 26 Mar 2006, 12:24
-
 par marocain94 » 11 Nov 2007, 11:11
par marocain94 » 11 Nov 2007, 11:11
bonjour j'ai besoin d'un peu d'aide pour cette exo merci d'avance !
je dois determiner les réels ;) et ;) tels que p(x)=x^4 - x³ + ;)x² + ;) admette 1-i comme racine et factoriser p(x) dans R(x)
est ce que je dois commencer par remplacer x par (1-i) pour simplifier l'expression?
-
marocain94
- Membre Relatif
- Messages: 116
- Enregistré le: 26 Mar 2006, 12:24
-
 par marocain94 » 11 Nov 2007, 11:22
par marocain94 » 11 Nov 2007, 11:22
je trouve p(x) = 4i + 1 + ;) (-2i) + ;) je trouve donc ;)=-4i et ;)= (1/2i)
est ce que c'est juste?
-
prody-G
- Membre Relatif
- Messages: 376
- Enregistré le: 28 Mar 2006, 14:36
-
 par prody-G » 11 Nov 2007, 11:29
par prody-G » 11 Nov 2007, 11:29
salut,
si
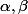
sont des réels ça ne peut pas être ça.
Tu sais que p(1-i)=0 et en remplaçant x par 1-i tu auras quelquechose de plus simple. Il te suffit alors d'isoler partie réelle et imaginaire. (je trouve :

)
-
marocain94
- Membre Relatif
- Messages: 116
- Enregistré le: 26 Mar 2006, 12:24
-
 par marocain94 » 11 Nov 2007, 11:43
par marocain94 » 11 Nov 2007, 11:43
la je trouve ;) =2 et ;)=-1 avec ;)+1 + i(-2;)+4) = 0
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 11 Nov 2007, 11:46
par tize » 11 Nov 2007, 11:46
Bonjour,
je confirme le résultat de prody-G,

-
marocain94
- Membre Relatif
- Messages: 116
- Enregistré le: 26 Mar 2006, 12:24
-
 par marocain94 » 11 Nov 2007, 11:53
par marocain94 » 11 Nov 2007, 11:53
je comprend pas j'ai pourtant bien calculé , alpha et béta sont des réels d'après l'énoncé 'jai mis sous forme X+iY et ensuite que c'est nul donc X=0 et Y=0
-
marocain94
- Membre Relatif
- Messages: 116
- Enregistré le: 26 Mar 2006, 12:24
-
 par marocain94 » 11 Nov 2007, 11:55
par marocain94 » 11 Nov 2007, 11:55
p(1-i) = 4i + 1 + ;) (-2i) + ;) si on remplace ;)=1 et ;)=2 sa marche pas?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 11 Nov 2007, 12:06
par tize » 11 Nov 2007, 12:06
non, moi j'ai
=(\beta-2)+i(2-2\alpha))
.
-
marocain94
- Membre Relatif
- Messages: 116
- Enregistré le: 26 Mar 2006, 12:24
-
 par marocain94 » 11 Nov 2007, 12:15
par marocain94 » 11 Nov 2007, 12:15
je confirme autan pour moi dsl, et pour la factorisation de p(x) dans R(x) je dois proceder comment?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 11 Nov 2007, 12:34
par tize » 11 Nov 2007, 12:34
Tu as déjà une racine de P.
P est à coefficient réelle, les racines complexes sont donc conjuguées, ensuite tu factorise.........
-
marocain94
- Membre Relatif
- Messages: 116
- Enregistré le: 26 Mar 2006, 12:24
-
 par marocain94 » 11 Nov 2007, 13:15
par marocain94 » 11 Nov 2007, 13:15
donc il faut factoriser par le conjugué de 1-i qui est 1+i??
-
marocain94
- Membre Relatif
- Messages: 116
- Enregistré le: 26 Mar 2006, 12:24
-
 par marocain94 » 11 Nov 2007, 13:35
par marocain94 » 11 Nov 2007, 13:35
peut-on utiliser la méthode de division euclidienne pour factoriser si oui il faut diviser par quoi?
-
marocain94
- Membre Relatif
- Messages: 116
- Enregistré le: 26 Mar 2006, 12:24
-
 par marocain94 » 11 Nov 2007, 13:52
par marocain94 » 11 Nov 2007, 13:52
p(x)=x^4 - x³ + ;)x² + ;) avec ;)=1 et ;)=2 donc p(x)=x^4 - x³ + x² + 2
Une racine de ce polynôme p est 1-i
Donc il existe un polynôme g tel que pour tout réel x p(x) = (x -(1-i)) . g(x).
Ce polynôme g est le quotient de la division euclidienne du polynôme f par le polynôme x + 2.
?????????????
-
prody-G
- Membre Relatif
- Messages: 376
- Enregistré le: 28 Mar 2006, 14:36
-
 par prody-G » 11 Nov 2007, 15:00
par prody-G » 11 Nov 2007, 15:00
Tu sais qu'un polynôme P de degré n est de la forme :
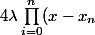)
où

est le coefficient dominant du polynôme et

une racine de P.
Tu sais que (1-i) et (1+i) sont racines de P, donc tu peux factoriser p(x) par (x-(1-i)) et (x-(1+i)), => p(x) = (x-(1-i))(x-(1+i))g(x) avec g un polynôme de degré 2 puisque p est de degré 4.
Donc g(x)=ax²+bx+c. Et il te reste à identifier a,b et c.
-
marocain94
- Membre Relatif
- Messages: 116
- Enregistré le: 26 Mar 2006, 12:24
-
 par marocain94 » 11 Nov 2007, 17:04
par marocain94 » 11 Nov 2007, 17:04
je trouve en fesant le division euclidienne de x^4 - x³ + x² + 2 par x²-2x+2 un quotient de x²+x+1 en fesant le produit quotient diviseur je trouve le dividende donc je pense avoir bon??
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
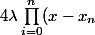) où
où  est le coefficient dominant du polynôme et
est le coefficient dominant du polynôme et  une racine de P.
une racine de P.