Recurrence
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
stofeul
- Membre Naturel
- Messages: 98
- Enregistré le: 12 Sep 2007, 17:44
-
 par stofeul » 09 Nov 2007, 18:35
par stofeul » 09 Nov 2007, 18:35
bonjour,je dois resoudre un petit exercice et je n'y arrive pas,pouvez vous m'aider svp...
sachant que u est definie par U0=0 et pour tout entier naturel n:
U n+1= ((racine de 2) / (2) )fois (racine de(1+Un))
demontrer par reucurrence que pour tout entier natuel n:
Un= cos ( ( pi )/ ( 2^n+1) )
merci bien
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 09 Nov 2007, 18:48
par Monsieur23 » 09 Nov 2007, 18:48
Une petite aide :
Tu as, si x est réel : 2 Cos²(x/2) = 1 + Cos(x)
« Je ne suis pas un numéro, je suis un homme libre ! »
-
stofeul
- Membre Naturel
- Messages: 98
- Enregistré le: 12 Sep 2007, 17:44
-
 par stofeul » 09 Nov 2007, 18:54
par stofeul » 09 Nov 2007, 18:54
je n'arrive pas à voir le rapport....
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 09 Nov 2007, 19:03
par Monsieur23 » 09 Nov 2007, 19:03
Pour n = 0, c'est bon.
Supposons OK pour le rang n.
 })
} ) })
J'te laisse conclure
« Je ne suis pas un numéro, je suis un homme libre ! »
-
nath59320
- Membre Relatif
- Messages: 337
- Enregistré le: 20 Sep 2006, 13:57
-
 par nath59320 » 09 Nov 2007, 19:18
par nath59320 » 09 Nov 2007, 19:18
je ne comprend pas pourquoi on fait cela, je ne voit pas ou on veut en venir
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 09 Nov 2007, 19:45
par Monsieur23 » 09 Nov 2007, 19:45
Je comprends pas vraiment la question là ... :hein:
Qu'est ce que tu ne comprends pas ?
« Je ne suis pas un numéro, je suis un homme libre ! »
-
nath59320
- Membre Relatif
- Messages: 337
- Enregistré le: 20 Sep 2006, 13:57
-
 par nath59320 » 09 Nov 2007, 19:52
par nath59320 » 09 Nov 2007, 19:52
ben je sais pas ou vous voulez en venir, enfin je ne vois pas quoi conclure
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 09 Nov 2007, 19:57
par Monsieur23 » 09 Nov 2007, 19:57
} ) })
Donc
} ) })
Or,

, donc

Donc
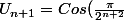)
, d'où l'hérédité de la propriété.
C'est bon ?
« Je ne suis pas un numéro, je suis un homme libre ! »
-
nath59320
- Membre Relatif
- Messages: 337
- Enregistré le: 20 Sep 2006, 13:57
-
 par nath59320 » 09 Nov 2007, 20:01
par nath59320 » 09 Nov 2007, 20:01
ahh ok, oula je n'aurai jamais reussi, merci bcp
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
