Mesure et integration
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ClaireD
- Membre Naturel
- Messages: 22
- Enregistré le: 22 Sep 2007, 14:12
-
 par ClaireD » 06 Nov 2007, 22:50
par ClaireD » 06 Nov 2007, 22:50
bonjour à tous .
On m'a donné un devoir et il ya une question que je n'arrive pas à faire :
Soit L2(R) l'espace des fontions f de carré intégrable sur R.
(f,g) =
^(+\infty)f(x)g(x)dx)
et
N(f)=
})
soit l une forme linéaire continue non nulle sur L2(R)
on a l(g) = sup { |l(f)| | N(f)=1}
Montrer que (f,g) = 0 avec f appartenant à L2(R) telle que l(f)=0
j'ai rédigé une réponse mais je crains que ce ne soit pas correct...
Si vous avez des suggestions , elles sont les bienvenues :happy2:
merci d'avance.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 06 Nov 2007, 23:08
par yos » 06 Nov 2007, 23:08
ClaireD a écrit:soit l une forme linéaire continue non nulle sur L2(R)
on a l(g) = sup { |l(f)| | N(f)=1}
Problème de définition il me semble.
-
ClaireD
- Membre Naturel
- Messages: 22
- Enregistré le: 22 Sep 2007, 14:12
-
 par ClaireD » 07 Nov 2007, 00:08
par ClaireD » 07 Nov 2007, 00:08
Non désolée c'est moi qui n'en est pas dit assez.
on considère une suite d'éléments gk tels que N(gk)=1
et lim l(gk) =sup { |l(f)| | N(f)=1}
alors on a montré precedemment que gk tend vers une limite g dans L2(R)
telle que l(g)=sup { |l(f)| | N(f)=1}
et N(g)=1
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 07 Nov 2007, 11:07
par yos » 07 Nov 2007, 11:07
ClaireD a écrit: |l(f)|
C'est ça que je ne comprends pas. Il y a deux normes différentes pour f ?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 07 Nov 2007, 11:21
par yos » 07 Nov 2007, 11:21
Ah oui, j'avais confondu un

avec une barre de valeur absolue : ça me semblait absurde.
Tu as donc

qui réalise la norme de

(norme subordonnée à celle de

). Tu dois prouver que
^\perp)
.
-
ClaireD
- Membre Naturel
- Messages: 22
- Enregistré le: 22 Sep 2007, 14:12
-
 par ClaireD » 07 Nov 2007, 14:19
par ClaireD » 07 Nov 2007, 14:19
effectivement j'ai voulu montrer que g appartenait a Ker(l)
Pour cela j'ai dit que comme l(g)=sup{|l(f)| | N(f) = 1 }
et que l est par hypothese une fonction non identiquement nulle , alors l(g) > 0 (mais dans ce cas je n'ai pas considéré qu N(f)=1 , est ce que ça change quelque chose ? )
Donc g n'appartient pas a ker(l)
comme nous sommes dans un espace hilbertien, g appartient a l'orthogonal de ker(l) tel que L2(R) = ortho(Kerl(l) +(somme directe) Ker(l)
par hyphothese , comme f appartient a Ker(l)
alors (g,f) = 0
cela est-t'il correct ?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 07 Nov 2007, 14:52
par yos » 07 Nov 2007, 14:52
Non ça ne va pas.
Si g n'est pas dans

, cela ne veut pas dire qu'il est dans son orthogonal!
J'ai voulu te dire que le problème devient un simple problème de géométrie.
Partons ainsi :

avec

et
^\perp)
.
On a donc
=\ell(v))
donc v réalise aussi la norme de

. Mais v est plus petit que g (en norme), donc si on le normalise en le multipliant par
,)
on obtient un vecteur
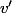
de norme 1 et qui vérifie
\geq \ell(v))
. C'est contradictoire, à moins que
=1)
, c'est-à-dire
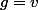
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
