Bon, je fais aussi l'autre sens, par contraposition.
Il s'agit alors de démontrer que
\vee\neg(q\to r)\to\neg(p\to r))
pour se faire, on suppose que l'on a
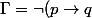\vee\neg(q\to r))
, il s'agit alors de démontrer que l'on a
)
Bon, pour avoir la négation de
)
, on peut tenter de démontrer que l'on obtient l'absurde (
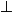
) en supposant que l'on a, en plus de

,
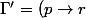)
.
En fait, à partir de

et
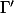
on alors
)
d'une part et grâce au fait que
=p\wedge\neg q)
, on obtient que l'on a

d'autre part.
Ainsi, on peut avoir

. Mais, grâce à
=q\wedge\neg r)
, on a aussi alors
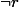
... belle contradiction !
Je mets ça en forme (plus comme moi là en ce moment) :
[CENTER]
}})
[/CENTER]
PS : au début, j'avais mis les
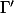
au lieu des

, mais c'était pas très lisible, alors j'ai tout remis
in extenso.