Espaces vectoriels

[laetiti36]

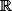
E et F st 2 sous espaces ectoriels de ^3, déterminer .
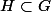
H= Vect (u,v) et G est un sous espace vectoriel de ^3. Comment montrer que et a-t-on G=H?
Comment, losque l'on a Imf, démontrer que f est surjective? ( avec Imf=F? mais dans ce cas comment?).
Merci de me donner des indications, des exemples, des solutions pour m'aider.

P.S: je suis en cpge B/L 1ére année

[Alex29]

:doh: je voudrais bien t'aider mais j'avoue que je n'ai pas tout compris dans ce que tu demandais : je vais essayer !!!


1) si tu as deux ev (espaces vectoriels) E et F, alors E inter F est bien un ev lui aussi tu peux le prouver toi même (tu montres que c'est un sous-ev de E par exemple) :
- tu dis bien que E inter F est non vide
- tu dis que E inter F est inclus dans E
- tu prouves la stabilité par combinaison linéaire

2) pour prouver qu'un ev est dans un autre, tu prends n'importe quel élément de H et tu prouves qu'il est aussi dans G.

et pour prouver G = H tu peux par exemple travailler par double inclusion.


3) pour la surjectivité, tout dépend de la situation mais soit tu as directement Imf = F (ev d'arrivée), soit tu déterminers à la main (avec la définition de l'image) l'image, ce qui est assez rare
On travaille plus facilement sur le noyau.

j'espère t'avoir aider un peu...