Equation exponentielle

[Yorck Horis]

Bonjour mon equation est e^((x-1)/x²) et j'ai du mal à trouver le signe de la dérivée seconde.

C'est peut-être du à une erreur de ma part donc voici mes réponses:

f'(x)= ((-x²+2)/x^4)*e^((x-1)/x²)

f"(x) = (e^((x-1)/x²))*((2x^3-5x^2-4x+4)/x^6)

Si vous pouviez m'aider, celà me serai bien utile.

Merci d'avance

[fibonacci]

Bonjour,

si la fct s'écrit

on a

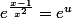
avec

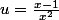
D'où la dérivée première:

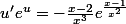
[Yorck Horis]

Oui j'avais oublier un x
f'(x)= ((-x²+2x)/x^4)*e^((x-1)/x²)

=> (-x+2)/x^3) e^((x-1)/x²)

Mais c'est la derivée seconde où je bloque

[fibonacci]

on tombe sous la forme UV avec
et

la dérivée est



=

[Yorck Horis]

merci de votre aide

Mais le probleme vient toujours de l'etude de signe de f"(x)

[fibonacci]

Bonjour;

Pouquoi l'étude def"'x)?; cela n'est pas nécessaire, sauf pour certains points particuliers et qui n'existent pas pour f'x).
:hum:

[Yorck Horis]

Car je dois faire le tableau des variations globale, donc j'ai besoin de f"(x).