DM math "casse tête"
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
pictbridge12
- Membre Naturel
- Messages: 19
- Enregistré le: 31 Oct 2007, 09:09
-
 par pictbridge12 » 31 Oct 2007, 09:28
par pictbridge12 » 31 Oct 2007, 09:28
Bonjour, mon DM est à rendre pour la rentrée des vacances
Le nombre d'or est la solution positive, noté µ de l'équation (e): x^2+x-1
1. Déterminer la valeur de µ
2. montrer que µ-1=1/µ
en déduire que 1/µ^2=2-µ
Remarque question 1 et 2 sont indépendantes
Je bloque sur la question 2 . pour la une je pense que c'est 3/2
-
Easyblue
- Membre Relatif
- Messages: 344
- Enregistré le: 07 Nov 2006, 15:39
-
 par Easyblue » 31 Oct 2007, 09:37
par Easyblue » 31 Oct 2007, 09:37
Bonjour,
Je suppose que ton équation est x²+x-1=0. Dans ce cas, ta solution est fausse. Quel est ton delta?
-
pictbridge12
- Membre Naturel
- Messages: 19
- Enregistré le: 31 Oct 2007, 09:09
-
 par pictbridge12 » 31 Oct 2007, 09:52
par pictbridge12 » 31 Oct 2007, 09:52
oui tu a raison delta=5 donc µ= 1+racine5/2
-
Easyblue
- Membre Relatif
- Messages: 344
- Enregistré le: 07 Nov 2006, 15:39
-
 par Easyblue » 31 Oct 2007, 10:12
par Easyblue » 31 Oct 2007, 10:12
Presque. Noublie pas que la formule dit :
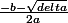
et
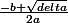
-
pictbridge12
- Membre Naturel
- Messages: 19
- Enregistré le: 31 Oct 2007, 09:09
-
 par pictbridge12 » 31 Oct 2007, 10:48
par pictbridge12 » 31 Oct 2007, 10:48
Le nombre d'or est la solution positive de l' équation x²+x-1=0 donc ici
il n'y a q'une solution
-
pictbridge12
- Membre Naturel
- Messages: 19
- Enregistré le: 31 Oct 2007, 09:09
-
 par pictbridge12 » 31 Oct 2007, 10:51
par pictbridge12 » 31 Oct 2007, 10:51
quelqun a une idée pour la question 2
-
Easyblue
- Membre Relatif
- Messages: 344
- Enregistré le: 07 Nov 2006, 15:39
-
 par Easyblue » 31 Oct 2007, 11:08
par Easyblue » 31 Oct 2007, 11:08
pictbridge12 a écrit:Le nombre d'or est la solution positive de l' équation x²+x-1=0 donc ici
il n'y a q'une solution
Oui je suis d'accord mais ce n'est pas 1... mais -1....
De plus tu as du faire une erreur pour la 2 dans l'énoncé
-
pictbridge12
- Membre Naturel
- Messages: 19
- Enregistré le: 31 Oct 2007, 09:09
-
 par pictbridge12 » 31 Oct 2007, 15:55
par pictbridge12 » 31 Oct 2007, 15:55
oui c'est vrai le nombre d'or est -1+racine5/2
:marteau:
mais pas d'erreur pour la question 2 il faut démontrer que 1-µ=1/µ
puis en déduire que 1/µ^2=2-µ
-
pictbridge12
- Membre Naturel
- Messages: 19
- Enregistré le: 31 Oct 2007, 09:09
-
 par pictbridge12 » 31 Oct 2007, 16:20
par pictbridge12 » 31 Oct 2007, 16:20
je me suis trompé dans l'énoncé c'est x^2-x-1 donc en fait µ=1+racine5/2
la question 2 est bonne
-
Easyblue
- Membre Relatif
- Messages: 344
- Enregistré le: 07 Nov 2006, 15:39
-
 par Easyblue » 31 Oct 2007, 16:24
par Easyblue » 31 Oct 2007, 16:24
Bien sûr quelle est bonne maintenant que tu as rectifié l'erreur :ptdr:
Alors as-tu une idée pour la 2 ?
-
pictbridge12
- Membre Naturel
- Messages: 19
- Enregistré le: 31 Oct 2007, 09:09
-
 par pictbridge12 » 31 Oct 2007, 16:29
par pictbridge12 » 31 Oct 2007, 16:29
:triste: aucune idée
-
Easyblue
- Membre Relatif
- Messages: 344
- Enregistré le: 07 Nov 2006, 15:39
-
 par Easyblue » 31 Oct 2007, 16:35
par Easyblue » 31 Oct 2007, 16:35

est solution de
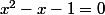
donc:
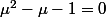
puis on divise tout par

et le travail est quasiment fini
-
pictbridge12
- Membre Naturel
- Messages: 19
- Enregistré le: 31 Oct 2007, 09:09
-
 par pictbridge12 » 31 Oct 2007, 16:47
par pictbridge12 » 31 Oct 2007, 16:47
donc:
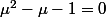
puis on divise tout par

et le travail est quasiment fini[/quote]
je vois pas ce que tu veux dire :help:
-
pictbridge12
- Membre Naturel
- Messages: 19
- Enregistré le: 31 Oct 2007, 09:09
-
 par pictbridge12 » 31 Oct 2007, 16:48
par pictbridge12 » 31 Oct 2007, 16:48
donc:
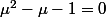
puis on divise tout par

[/quote]
je vois pas ce que tu veux dire :help:
-
pictbridge12
- Membre Naturel
- Messages: 19
- Enregistré le: 31 Oct 2007, 09:09
-
 par pictbridge12 » 31 Oct 2007, 16:49
par pictbridge12 » 31 Oct 2007, 16:49
donc:
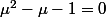
puis on divise tout par

je vois pas ce que tu veux dire :help:
-
Easyblue
- Membre Relatif
- Messages: 344
- Enregistré le: 07 Nov 2006, 15:39
-
 par Easyblue » 31 Oct 2007, 16:52
par Easyblue » 31 Oct 2007, 16:52
-
pictbridge12
- Membre Naturel
- Messages: 19
- Enregistré le: 31 Oct 2007, 09:09
-
 par pictbridge12 » 31 Oct 2007, 17:07
par pictbridge12 » 31 Oct 2007, 17:07
donc ça donne µ-1-1/µ=0
µ-1=1/µ
-
pictbridge12
- Membre Naturel
- Messages: 19
- Enregistré le: 31 Oct 2007, 09:09
-
 par pictbridge12 » 31 Oct 2007, 17:41
par pictbridge12 » 31 Oct 2007, 17:41
je trouve donc µ-1-1/µ=0
µ-1=1/µ
puis il faut déduire que 1/u^2=2-µ
-
Easyblue
- Membre Relatif
- Messages: 344
- Enregistré le: 07 Nov 2006, 15:39
-
 par Easyblue » 31 Oct 2007, 17:43
par Easyblue » 31 Oct 2007, 17:43
C'est facile ça, non?
l faut encore diviser par

(de chaque côté du =, j'espère que tu comprend cette fois :marteau: )
-
pictbridge12
- Membre Naturel
- Messages: 19
- Enregistré le: 31 Oct 2007, 09:09
-
 par pictbridge12 » 31 Oct 2007, 17:55
par pictbridge12 » 31 Oct 2007, 17:55
Je sais je suis lourd :mur:
donc il faut faire µ-1/µ =
et (1/µ)/µ = 1/µ*1/µ = 1/µ^2
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
