Arithmétique TS spe , curiosité

[sqrt]

bonsoir,

j'ai été attiré par une remarque:

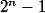
si N (entier naturel) est de la forme avec premier , alors N est un nombre parfait.

en fait j'ai eu l'idée de décomposer et d'exprimer la somme des diviseurs stricts de N mais ca ne m'a pas mené à de jolies choses.

autre problème:

au jour d'aujourd'hui on ne sait pas s'il existe des nombres parfaits impairs cependant est ce qu'il serait facile de prouver que s'il existe alors nécessairement ils sont supérieurs à . là j'avoue je reste muet .

merci

[Joker62]

Les diviseurs de 2^n - 1 sont 1 et 2^n - 1 car premier

Reste donc la somme des divisieurs de 2^(n-1)
Les diviseurs de ça, c'est 2^k avec k compris entre 0 et n-1

La somme des 2^k pour k allant de 0 à n-1, se calcule facilement ( suite géométrique )

On peut alors faire la somme !
Ne pas oublier d'enlever un 1 car sinon, on le compterai deux fois ;)

[sqrt]

il faut calculer la somme des diviseurs stricts donc k varie entre 0 et n-2 ?

[Joker62]

Si c'est strict alors oui c'est bien n-2
Et il faut alors enlever le 2^n - 1
J'avais oublier la déf désolé ;)

[sqrt]

oui c'est bon je trouve bien une somme égale au nombre

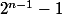
merci