bonjour tout le monde
les maths en 1èr S c'est dur dur....
j'aurais besoin d'un coup de main
pour l'exercice 56 :
.
.
on considère de cercle C d'équation
x^2+2x+y^2-y=5
et le cercle T de centre F(4;3) et de rayon 5.
1) déterminer le centre et le rayon du cercle C et une équation de cercle T.
2) tracer C et T sur une meme figure.
3) calculer les coordonnées des points d'intersection A et B des deux cercles.
.
.
.
1) j'ai mis que l'équation d'un cercle dans un plan est la meme que celle d'un cylindre dans l'espace d'où :
x^2 + y^2 = R^2
donc 4^2 + 3^2 = 5^2
c'est comme ça qu'il faut présenter ?
et pour déterminer le centre et le rayon du cercle C, ne ne comprend pas non plus comment je dois faire...
ensuite pour les autre questions si j'arrive à trouver les deux équations des cercles je pense pourvoir y arriver...
merci d'avance si vous me donner un coup de main
Encore un peu d'aide svouplé....
11 messages
- Page 1 sur 1
ALors le but de la premiere question de la question 1 va être de mettre l'équation
x²+2x+y²-y=5
sous
la forme
(x-a)²+(y-b)²=R²
On voit déja que l'équation commence par
x²+2x
On va faire apparaitre un produit remarquable pour factoriser
On voit que c'est le début de (x+1)²=x²+2x+1
Il nous manque le +1 qu'importe on l'introduit:
x²+2x+y²-y=x²+2x +1-1 +y²-y
donc au final cela devient: (x+1)²-1+y²-y=5
Soit (x+1)²+y²-y=6
Reste à factoriser la deuxieme partie:

Donc cela ressemble au début de^{2}=y^{2}-y+\frac{1}{4})
Il nous manque le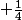
qu'importe on l'introduit:


donc finalement:
l'équation devient
^{2} +(y-\frac{1}{2})^{2}=6+\frac{1}{4}=\frac{25}{4})
Donc ceci est une équation du cercle de centre (-1;1/2) et de rayon 5/2.
x²+2x+y²-y=5
sous
la forme
(x-a)²+(y-b)²=R²
On voit déja que l'équation commence par
x²+2x
On va faire apparaitre un produit remarquable pour factoriser
On voit que c'est le début de (x+1)²=x²+2x+1
Il nous manque le +1 qu'importe on l'introduit:
x²+2x+y²-y=x²+2x +1-1 +y²-y
donc au final cela devient: (x+1)²-1+y²-y=5
Soit (x+1)²+y²-y=6
Reste à factoriser la deuxieme partie:
Donc cela ressemble au début de
Il nous manque le
qu'importe on l'introduit:
donc finalement:
l'équation devient
Donc ceci est une équation du cercle de centre (-1;1/2) et de rayon 5/2.
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 91 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
