Géométrie dans un plan.

par **chonry** » 29 Oct 2007, 16:08

J'ai un exercice a faire et j'ai du mal. Merci de bien vouloir m'aider pour que je comprenne.

Dans un plan, C est un demi-cercle de diamètre [AB] et de centre O.
P est un point qui appartient à C. C1 est le cercle de centre A qui passe par P ; il coupe la droite (AB) en M et N. G1 et G sont les centres de gravité respectifs des triangles ABP et MNP.
-->
1. Démontrer que le vecteur G1G reste constant lorsque P décrit le demi-cercle C
2. a) Démontrer que la parallèle à la droite (PO) qui passe par G coupe la droite (AB) en un point E.
b) Exprimer la distance EG1 en fonction de AB.
c) En déduire le lieu des points G1 lorsque P décrit le demi-cercle C.

Merci de m'aider car j'ai beau chercher je n'y arrive pas.

par **Easyblue** » 29 Oct 2007, 16:21

Bonjour,
pour la première question, il faut que tu arrives à montrer que

ne dépend pas de P. Pour cela il faut que tu écrives ce que c'est dêtre l'isobarycentre d'un triangle.

par **Noemi** » 29 Oct 2007, 16:30

Il faut exprimer le vecteur G1G en fonction d'un vecteur faisant appel aux points fixes O, A et B.
Utilise la relation de Chasles.

par **chonry** » 29 Oct 2007, 16:54

Oui je sui d'accord. J'ai déja dit que G barycentre de (A,1) (B,1) (P,1)
G1 barycentre de (M,1) (N,1) (P,1)
J'ai donc fait des associations G barycentre de (O,2) (P,1)
G1 barycentre de (A,2) (P,1)
Mais je bloque je n'arrive pas a voir la situation... merci de m'expliquer

par **Easyblue** » 29 Oct 2007, 17:00

Personellement, je suis parti en écrivant

et

puis en utilisant chasles je suis arriver à quequechose qui dépend que de

par **chonry** » 29 Oct 2007, 17:01

pourquoi 3...?

par **Easyblue** » 29 Oct 2007, 17:05

D'apès ton cours, tu dois avoir un truc dans ce genre:
Si G est l'isobarycentre de {A,B,C} alors

par **chonry** » 29 Oct 2007, 17:09

A non désolé je ne connaissait pas cette formule.

par **Easyblue** » 29 Oct 2007, 17:10

Alors comment écris tu avec des vecteurs que G est lisobarycentre de A,B,C

par **chonry** » 29 Oct 2007, 17:12

aGA +bGB +cGC = O (vecteur nul)

par **Easyblue** » 29 Oct 2007, 17:26

Oui et en locurence comme la on parle disobarycentre a=b=c=1. Mais si tu utilise Chasles avec un point O, tu verra qu'on retombe sur la formule que je t'es mis au dessu

par **chonry** » 29 Oct 2007, 17:32

Aidez moi s'il vous plait.

par **Easyblue** » 29 Oct 2007, 17:34

G est l'isobarycentre de MNP donc on peut écrire :

Essaye de suivre le même raisonnement avec

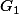
isobarycentre de ABP

par **chonry** » 29 Oct 2007, 17:50

d'acco'rd je vais aisseyer
je reviendrais demain merci beaucoup

Géométrie dans un plan.

Géométrie dans un plan.

Qui est en ligne