bonjour
c'est ma premiére sur ce gentil forum.
la réponse à la question qui m'améne doit etre perdu au fin fond de moi, et j'ai besoin de vous pour m'aider a la trouver :)
il sagit simplement de dégrader un pic egal a 1
je suis en train de programmer un tableau de t elements qui devra
1) avoir une somme = 1
2) etre remplis de reels compris entre 0 et 1
3) je souhaite avoir un dégradé de valeur Et la somme des valeurs égal a 1.
ex
.14----.14-----.14----.14----.14----.14----.14 constant ?
1------0------0------0------0------0------0 lineaire ?
.6-----.3------.1-----0------0------0------0
.5-----.3------.1-----.75----.15----.07----.03
.03----.07-----.2-----.4-----.2-----.07----.03 parabolique ?
etc
j'imagine qu'il doit y avoir plusieur solution pour resoudre ce probleme
peut etre qu'avec une suite recurente :p ??? je sais plus comment ca marche.
aurevoir
eky.
Somme de n reel R[0;1] = 1
11 messages
- Page 1 sur 1
bjr,
comment faire ?
quelques outils:
- toute somme de n termes positifs , divisés par leur somme
- une loi de probabilité (la somme des probas vaut 1 et chaque proba est positive)
- un polynôme de Bernstein
- une somme d'une intégrale d'une fonction positive
avec
 ,sommée sur une subdivision de [0,1]
,sommée sur une subdivision de [0,1]
exemples:
})

dt } { \int_{0}^{1} f(t)dt})

car:

la suite (b) donne des nombres décimaux.
Le problème général, c'est qu'il faut arrondir les valeurs obtenues pour avoir
des décimaux et reporter les arrondis sur le dernier terme de la somme,
un peu comme pour les tableaux d'amortissement.
Alors le must, ce sont les polynômes de Bernstein:
http://orion3d.alrj.org/articles/files/courbes_surf/node3.html
on prend pour un nombre décimal de ]0,1[, les coefficients
un nombre décimal de ]0,1[, les coefficients
du binôme sont des entiers.
On peut ensuite générer une permutation aléatoire des n termes
pour donner une impression de chaos. :mur:
cordialement,
comment faire ?
quelques outils:
- toute somme de n termes positifs , divisés par leur somme
- une loi de probabilité (la somme des probas vaut 1 et chaque proba est positive)
- un polynôme de Bernstein
- une somme d'une intégrale d'une fonction positive
avec
exemples:
car:
la suite (b) donne des nombres décimaux.
Le problème général, c'est qu'il faut arrondir les valeurs obtenues pour avoir
des décimaux et reporter les arrondis sur le dernier terme de la somme,
un peu comme pour les tableaux d'amortissement.
Alors le must, ce sont les polynômes de Bernstein:
http://orion3d.alrj.org/articles/files/courbes_surf/node3.html
on prend pour
du binôme sont des entiers.
On peut ensuite générer une permutation aléatoire des n termes
pour donner une impression de chaos. :mur:
cordialement,
J'ai peur que la plupart de tes outils soient beaucoup trop lourd pour moi.
aprés les avoir compris, il fodra que je les programmes.
Imagine que je devrai faire un programme qui devra utiliser ses outils a ma place, pour resoudre le probléme. heu c dur :mur:
je pense que resoudre une integration = 1 d'un fonction positive suffira amplement.
mais pourquoi sur une subdivision de [0,1]
Ok mais comment résoudre ca ?
comment etre sur que l'air délimité par des fontions>0 bien choisie serra égal a 1 ?
si j'ai 10 elements dans mon tableau.
je devrai prendre la valeur de l'air pour chaque tranche 0,1 dans l'interval [0;1]
j'ai l'impression que ca se tient, et j'aimerai bien y arriver, mais je crois que je manque de rigueur.
ps : comment on fait pour mettre des images screenshot de formules dans le texte ??
merci,
aprés les avoir compris, il fodra que je les programmes.
Imagine que je devrai faire un programme qui devra utiliser ses outils a ma place, pour resoudre le probléme. heu c dur :mur:
je pense que resoudre une integration = 1 d'un fonction positive suffira amplement.
mais pourquoi sur une subdivision de [0,1]
Ok mais comment résoudre ca ?
comment etre sur que l'air délimité par des fontions>0 bien choisie serra égal a 1 ?
si j'ai 10 elements dans mon tableau.
je devrai prendre la valeur de l'air pour chaque tranche 0,1 dans l'interval [0;1]
j'ai l'impression que ca se tient, et j'aimerai bien y arriver, mais je crois que je manque de rigueur.
ps : comment on fait pour mettre des images screenshot de formules dans le texte ??
merci,
ok :)
je suis ravi que tu m'aide
comment injectes tu des formules dans le forums?
je suis graphiste 3D et resoudre ce probleme me permetera de "strecher" un elastique.
quand tu tire dessus il ya des parties qui s'etendent plus ou moins.
(en fonction du fameux tableau)
Avec ta derniére formule, comment je fais pour deplacer le pic de souplesse de mon elastique ?
et comment faire pour qu'il soit souple aux extrémités et rigide au centre ?
Il ya des chose que je ne connais pas.
heu le C(k,n) la ? c'est la permutation ?
Le nombre de combinaison de n element dans un ensemble de k elements ?
mais le b(n,k) je n'ai jamais vu cela.
merci,
eki
je suis ravi que tu m'aide
comment injectes tu des formules dans le forums?
je suis graphiste 3D et resoudre ce probleme me permetera de "strecher" un elastique.
quand tu tire dessus il ya des parties qui s'etendent plus ou moins.
(en fonction du fameux tableau)
Avec ta derniére formule, comment je fais pour deplacer le pic de souplesse de mon elastique ?
et comment faire pour qu'il soit souple aux extrémités et rigide au centre ?
Il ya des chose que je ne connais pas.
heu le C(k,n) la ? c'est la permutation ?
Le nombre de combinaison de n element dans un ensemble de k elements ?
mais le b(n,k) je n'ai jamais vu cela.
merci,
eki
comment on utilise cette formule.
salut

j'aimerai que l'on m'explique comment fonctionne cette formule.
j'y comprend rien.
il parait que je pourrais en avoir besoin pour remplir un tableau, avec des valeurs toutes positives et inferieures à 1 et dont la somme du tableau est egale à 1.
merci,
j'aimerai que l'on m'explique comment fonctionne cette formule.
j'y comprend rien.
il parait que je pourrais en avoir besoin pour remplir un tableau, avec des valeurs toutes positives et inferieures à 1 et dont la somme du tableau est egale à 1.
merci,
eky a écrit:comment injectes tu des formules dans le forums?
C'est du code latex, que l'on entoure d'une balise TEX
eky a écrit:comment faire pour qu'il soit souple aux extrémités et rigide au centre ?
Si cette famille de coefficients doit être proportionnelle aux déformations,
les coefficients du binôme donneront une plus grande déformation au centre,
Pour un grand nombre de coefficients, les coefficients se répartissent comme une courbe en cloche.
eky a écrit:
heu le C(k,n) la ? c'est la permutation ?
Le nombre de combinaison de n element dans un ensemble de k elements ?
c'est le nombre de combinaison de k elements dans un ensemble de n elements
le numérateur et le dénominateur du quotient comporte
chacun k facteurs.
eky a écrit:
mais le b(n,k) je n'ai jamais vu cela.
la notation b(n,k)... était là juste pour distinguer les différentes familles de coefficients dans les exemples cités.
par contre, il y a peut être une formule intéressante:
les polynômes de Bernstein
cette somme de coeff. positifs vaut toujours 1.
Et pour l'animation, on peut faire varier l'entier n dans
eky a écrit:
quand tu tire dessus il ya des parties qui s'etendent plus ou moins.
(en fonction du fameux tableau)
Les coeff. du binome sont plus grands au centre qu'au bord. Si ces coefficients gèrent l'extension et non l'amplitude de la déformation, ça devrait être ok.
La formule pour programmer les coeff. du binome est soit:

chaque terme du triangle de Pascal est la somme du terme au dessus
et du terme au dessus à gauche,ce qui permet de passer d'une
ligne à l'autre:
1
1 2 1 (n=2)
1 3 3 1 (n=3)
1 4 6 4 1 (n=4)
1 5 10 10 5 1 (n=5)
1 6 15 20 15 6 1 (n=6)
1 7 21 35 35 21 7 1 (n=7)
et l'on divise les coeff de la ligne n par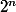
sinon, on peut calculer les coefficients d'une même ligne (n fixé)
par la récurrence sur l'entier k:

ce qui permettrait de calculer de proche en proche une déformation donnée.
(avec ces formules, il n'y aucun problème d'arrondis, les résultats sont des valeurs entières)
ensuite, on peut tester une permutation aléatoire des coeffs. en randomisant
les indices du tableau, histoire de voir l'effet graphique produit (joie, peur, vitesse, horreur ?)
PS: signalons aussi la courbe de la fonction)
qui condense toutes les sinusoïdes de la fonction sinus au voisinage de x=0
(effet comique)
chaque terme du triangle de Pascal est la somme du terme au dessus
et du terme au dessus à gauche,ce qui permet de passer d'une
ligne à l'autre:
1
1 2 1 (n=2)
1 3 3 1 (n=3)
1 4 6 4 1 (n=4)
1 5 10 10 5 1 (n=5)
1 6 15 20 15 6 1 (n=6)
1 7 21 35 35 21 7 1 (n=7)
et l'on divise les coeff de la ligne n par
sinon, on peut calculer les coefficients d'une même ligne (n fixé)
par la récurrence sur l'entier k:
ce qui permettrait de calculer de proche en proche une déformation donnée.
(avec ces formules, il n'y aucun problème d'arrondis, les résultats sont des valeurs entières)
ensuite, on peut tester une permutation aléatoire des coeffs. en randomisant
les indices du tableau, histoire de voir l'effet graphique produit (joie, peur, vitesse, horreur ?)
PS: signalons aussi la courbe de la fonction
qui condense toutes les sinusoïdes de la fonction sinus au voisinage de x=0
(effet comique)
je te remercie pour toute cette attention le busard des roseaux.
le truc c'est qu'avant d'aller plus loin, il faudrait que l'on soit sur du resultat que l'on veut obtenir.
Mon elastique est une suite de segments qui vont s'alonger plus ou moins.
J'aimerai pouvoir faire varier le long de l'elastique (un peu comme avec un curseur) la position qui (plus fragile) serra deformée.
1° Déplacer la cloche de valeurs des coeffs le long de mon elastique
2° Modifier l'amplitude de la cloche
3° inverser la cloche
sa serrait super si
n serait le nombre de segment de mon elastique (ou de coeffs dans le tableau) ?
t serait le curseur qui positionnerait sur l'elastique, le sommet de la cloche d'allongement ?
Modifier l'amplitude de la cloche ? c'est possible avec cette formule.
merci,
eky
le truc c'est qu'avant d'aller plus loin, il faudrait que l'on soit sur du resultat que l'on veut obtenir.
Mon elastique est une suite de segments qui vont s'alonger plus ou moins.
J'aimerai pouvoir faire varier le long de l'elastique (un peu comme avec un curseur) la position qui (plus fragile) serra deformée.
1° Déplacer la cloche de valeurs des coeffs le long de mon elastique
2° Modifier l'amplitude de la cloche
3° inverser la cloche
busard_des_roseaux a écrit:
les polynômes de Bernstein
cette somme de coeff. positifs vaut toujours 1.
Et pour l'animation, on peut faire varier l'entier n danspour le nombre de points et le paramètre t dans [0;1]
sa serrait super si
n serait le nombre de segment de mon elastique (ou de coeffs dans le tableau) ?
t serait le curseur qui positionnerait sur l'elastique, le sommet de la cloche d'allongement ?
Modifier l'amplitude de la cloche ? c'est possible avec cette formule.
merci,
eky
A la calculatrice:
chaque polynome de la somme intervient pour un coefficient (n+1
coeff. en tout).
l'entier n permet de faire varier l'amplitude de la cloche
le réel t déplace la cloche vers la gauche ou la droite
en t=0,5, on a une cloche symétrique, les termes centraux étant prépondérants
() .
.
Au fur et à mesure que t s'éloigne de 0,5 pour se rapprocher des extrémités du segment [0,1], le nombre de termes significatifs de la somme diminue.
en t voisin de zéro le poids de l'ensemble est déporté vers le dernier terme (k=n) et inversement , pour t voisin de 1, le poids est déporté vers le premier terme (k=1)
La suite de coeff:

est la cloche symétrique obtenue pour t=0,5.
chaque polynome de la somme intervient pour un coefficient (n+1
coeff. en tout).
l'entier n permet de faire varier l'amplitude de la cloche
le réel t déplace la cloche vers la gauche ou la droite
en t=0,5, on a une cloche symétrique, les termes centraux étant prépondérants
(
Au fur et à mesure que t s'éloigne de 0,5 pour se rapprocher des extrémités du segment [0,1], le nombre de termes significatifs de la somme diminue.
en t voisin de zéro le poids de l'ensemble est déporté vers le dernier terme (k=n) et inversement , pour t voisin de 1, le poids est déporté vers le premier terme (k=1)
La suite de coeff:
est la cloche symétrique obtenue pour t=0,5.
comment transformer la cloche.
merci, le busard des roseaux,
la formule que tu m'as donné marche du feu de dieu.
seulement, j'aimerai bien effectuer quelques opérations, pour modifier la cloche.
j'ai essayé d'inverser les coefficients de facon a ce que les parties qui s'étirent soient sur les bords.
j'ai fait :coeff[a] = (1-coeff[a])/(nbDeCoeff-1)
Logiquement la somme des coeffs du tableau vaut toujours 1
((1-1/4) + (1-1/4) + (1-1/4) + (1-1/4))/3 =1 (je suis partie de cette idée)
(3/4 + 3/4 +3/4 + 3/4)/3 =1
mais evidement ca n'inverse pas !
tu as peut etre une solution ?
une opération sur les coeffs du tableau ?
merci,
eky
la formule que tu m'as donné marche du feu de dieu.
seulement, j'aimerai bien effectuer quelques opérations, pour modifier la cloche.
j'ai essayé d'inverser les coefficients de facon a ce que les parties qui s'étirent soient sur les bords.
j'ai fait :coeff[a] = (1-coeff[a])/(nbDeCoeff-1)
Logiquement la somme des coeffs du tableau vaut toujours 1
((1-1/4) + (1-1/4) + (1-1/4) + (1-1/4))/3 =1 (je suis partie de cette idée)
(3/4 + 3/4 +3/4 + 3/4)/3 =1
mais evidement ca n'inverse pas !
tu as peut etre une solution ?
une opération sur les coeffs du tableau ?
merci,
eky
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
