FOnctions
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Bertrand Hamant
- Membre Rationnel
- Messages: 618
- Enregistré le: 02 Sep 2005, 14:14
-
 par Bertrand Hamant » 20 Sep 2005, 20:50
par Bertrand Hamant » 20 Sep 2005, 20:50
Bonjour je faisais cet exercice je l'ai presque terminé.
La fonction x^3 -3x²-9x+2
a une équation tangente de -9x-2, Montrer qu'il existe 2 tangents perpendiculaires à la droite d, précizez les abscisses des points de tangence,je bloque ici merci
-
Bertrand Hamant
- Membre Rationnel
- Messages: 618
- Enregistré le: 02 Sep 2005, 14:14
-
 par Bertrand Hamant » 20 Sep 2005, 21:41
par Bertrand Hamant » 20 Sep 2005, 21:41
Je ne vois pas comment on peut résoudre ce petit problème car je ne connais pas encore la formule de de l'orthogonalité
-
Galt
- Membre Rationnel
- Messages: 789
- Enregistré le: 13 Aoû 2005, 12:03
-
 par Galt » 20 Sep 2005, 21:46
par Galt » 20 Sep 2005, 21:46
Deux droites sont orthogonales si et ssi leurs coefficients directeurs ont pour produit -1
-
Ismail
- Membre Relatif
- Messages: 147
- Enregistré le: 07 Juin 2005, 22:12
-
 par Ismail » 20 Sep 2005, 21:56
par Ismail » 20 Sep 2005, 21:56
Bertrand Hamant a écrit:Bonjour je faisais cet exercice je l'ai presque terminé.
La fonction x^3 -3x²-9x+2
a une équation tangente de -9x-2, Montrer qu'il existe 2 tangents perpendiculaires à la droite d, précizez les abscisses des points de tangence,je bloque ici merci
peux tu etre plus clair dans ton énoncé?
c quoi la droite d ?
-
danskala
- Membre Relatif
- Messages: 129
- Enregistré le: 06 Mai 2005, 16:48
-
 par danskala » 20 Sep 2005, 21:59
par danskala » 20 Sep 2005, 21:59
salut,
le coefficient directeur de la droite d'équation y=-9x-2 est -9
le coefficient directeur de la tangente à la courbe de au point d'abscisse x est f '(x).
bye.
-
Bertrand Hamant
- Membre Rationnel
- Messages: 618
- Enregistré le: 02 Sep 2005, 14:14
-
 par Bertrand Hamant » 20 Sep 2005, 22:03
par Bertrand Hamant » 20 Sep 2005, 22:03
soit f (x) = x^3 -3x² -9x + 2
y = -9x -2
J'ai déterminé qu'au Point A ( 2 ; - 20 ) les deux droites en leurs points communs. Je dois montrer qu'il existe deux tangentes à Cf perpendiculaires à la droite d, Précisez les points de tangences.
on doit avoir f ' ( 2 ) * f ' ( x ) = -1
f ' ( 2 ) = -9 donc f ' ( x ) = 1/9
comment continuer après
-
danskala
- Membre Relatif
- Messages: 129
- Enregistré le: 06 Mai 2005, 16:48
-
 par danskala » 20 Sep 2005, 22:12
par danskala » 20 Sep 2005, 22:12
=3x^2-6x-9)
\times f'(x)=-1)
=-1)
Tu te retrouves avec une équation du second degré qu'il te reste à résoudre.
Bye
-
Bertrand Hamant
- Membre Rationnel
- Messages: 618
- Enregistré le: 02 Sep 2005, 14:14
-
 par Bertrand Hamant » 20 Sep 2005, 22:20
par Bertrand Hamant » 20 Sep 2005, 22:20
ça tombe pas juste
avec f ' ( 2 ) * f' ( x ) = -1
je trouve f ( ' x ) = 1/9
au point 2 on a donc 2/9 = -20
1/9x - 182/2 = y
-
danskala
- Membre Relatif
- Messages: 129
- Enregistré le: 06 Mai 2005, 16:48
-
 par danskala » 20 Sep 2005, 22:30
par danskala » 20 Sep 2005, 22:30
\times f'(x)=-1\Longleftrightarrow -9\times f'(x)=-1 \Longleftrightarrow f'(x)=\frac{1}{9})
Jusqu'ici je suis d'accord avec toi.
Mais ensuite, il faut bien résoudre cette équation :
=\frac{1}{9})
Et pour résoudre cette équation il faut remplacer f '(x) par 3x²-6x-9
Ce qui nous donne bien une équation du second degré
-
Bertrand Hamant
- Membre Rationnel
- Messages: 618
- Enregistré le: 02 Sep 2005, 14:14
-
 par Bertrand Hamant » 20 Sep 2005, 22:38
par Bertrand Hamant » 20 Sep 2005, 22:38
on trouve
x = -1 et x = 3
donc f ( -1 ) = 7 et f ( 3 ) = -25
f ' ( x ) = 1/9
7 = -1/9 + b
-25 = 1/3 + b
Ce sont les 2 équations tangentes. est ce bon ou il fallait résoudre 3x²-6x - 9 = 1/9
soit 3x² -6x -82/9 = 0 merci de répondre
-
danskala
- Membre Relatif
- Messages: 129
- Enregistré le: 06 Mai 2005, 16:48
-
 par danskala » 20 Sep 2005, 22:49
par danskala » 20 Sep 2005, 22:49
pour trouver x=-1 et x=3 tu as résolu f '(x)=0
Donc f '(-1) est égal à 0 et non pas à 1/9
Il faut donc bien résoudre
=1/9)
soit
=1)
soit

soit
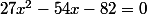
-
Bertrand Hamant
- Membre Rationnel
- Messages: 618
- Enregistré le: 02 Sep 2005, 14:14
-
 par Bertrand Hamant » 20 Sep 2005, 22:54
par Bertrand Hamant » 20 Sep 2005, 22:54
je trouve x1 = 54 + V11772/54
x2= 54-V11772/54
-
Bertrand Hamant
- Membre Rationnel
- Messages: 618
- Enregistré le: 02 Sep 2005, 14:14
-
 par Bertrand Hamant » 20 Sep 2005, 22:56
par Bertrand Hamant » 20 Sep 2005, 22:56
en somme ça revient à résoudre 3x²-6x-9, donc mes équations précédentes étaient bonnes
-
danskala
- Membre Relatif
- Messages: 129
- Enregistré le: 06 Mai 2005, 16:48
-
 par danskala » 20 Sep 2005, 23:04
par danskala » 20 Sep 2005, 23:04
OK pour x1 et x2
on trouve x1 environ égal à 3,009237...
et x2 environ égal à -1,0092379...
x1 n'est pas égal à 3 et x2 n'est pas égal à -1.
résoudre 3x²-6x-9=0 (comme tu l'as fait) ne revient absolument pas à résoudre 3x²-6x-9=1/9 ,même si les solutions de ces deux équations sont proches.
-
Bertrand Hamant
- Membre Rationnel
- Messages: 618
- Enregistré le: 02 Sep 2005, 14:14
-
 par Bertrand Hamant » 21 Sep 2005, 12:32
par Bertrand Hamant » 21 Sep 2005, 12:32
alors mes éuqations tangentes sont fausses. pour calculer 3x²-6x-9, j'ai fait avec delta les solutions son très proches comme faire alors
-
Bertrand Hamant
- Membre Rationnel
- Messages: 618
- Enregistré le: 02 Sep 2005, 14:14
-
 par Bertrand Hamant » 21 Sep 2005, 17:06
par Bertrand Hamant » 21 Sep 2005, 17:06
Qu'en pensez-vous alors ?
Puis je le faire avec x1 et x2 pour calculer les tangentes
-
Bertrand Hamant
- Membre Rationnel
- Messages: 618
- Enregistré le: 02 Sep 2005, 14:14
-
 par Bertrand Hamant » 21 Sep 2005, 18:22
par Bertrand Hamant » 21 Sep 2005, 18:22
Je pense qu'on peut avec x1 = -1 et x2 = 3
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 135 invités
