Bonjour !
J'aurais besoin d'éclaircissements concernant quelques exercices sur les congruences que voici :
Note : pour le symbole "congru", je n'ai rien trouvé de mieu que cette magnifique lettre grecque ;) .
1) Déterminez tout les entiers n, tels que n²-3n+6 soit divisible par 5.
2) Démontrez que pour tout entier naturel n : 4^n+6n-1 ;) 0 (mod 9)
3) Déterminez les entiers naturels pour lesquels : n*7^n + 4n + 1 est divisible par 8.
On m'a dit qu'il étaient faciles, mais ça fait quelques soirées que je nages... :hum:
Si quelqu'un a des idées concernant ces exercices, qu'il n'hésite pas ! Je cherche avant tout à les comprendre car je suis sensée savoir en faire de plus compliqués dans mon prochain devoir...
Merci d'avance !
Exercices congruences spé-maths
10 messages
- Page 1 sur 1
Bonsoir,
Le premier :
On remarque que n²-3n+6=n²+2n+1+5-5n
Ainsi, pour que 5 divise n²-3n+6, il faut et il suffit que 5 divise n²+2n+1, ie 5 divise (n+1)² donc par le théorème de Gauß que 5|n+1 et au final n est de la forme 5k-1.
Le deuxième :
On raisonne modulo 9 :
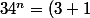^{n})
On réfléchit un peu.
On sait que^{n}=\Bigsum_{k=0}^{n} C_{n}^{k} 3^{k})
Or, dès que k est plus grand que 2, 3^k=0. On en déduit que^{n}=1+C_{n}^{1}3=1+3n)
D'où :

Essaye de faire le troisième :happy3:
Le premier :
On remarque que n²-3n+6=n²+2n+1+5-5n
Ainsi, pour que 5 divise n²-3n+6, il faut et il suffit que 5 divise n²+2n+1, ie 5 divise (n+1)² donc par le théorème de Gauß que 5|n+1 et au final n est de la forme 5k-1.
Le deuxième :
On raisonne modulo 9 :
On réfléchit un peu.
On sait que
Or, dès que k est plus grand que 2, 3^k=0. On en déduit que
D'où :
Essaye de faire le troisième :happy3:
salut,
tu connais la formule du binôme de newton ?
Sinon, pour le dernier :
on remarque que 7=(-1) [8]
donc que n*7^n = -n [8] quand n est impair
et
n*7^n = n [8] quand n est pair
deux cas donc :
1) n impair
n*7^n + 4n + 1 = 3n + 1 [8]
3n + 1 = 0 [8] 3n = -1 [8] 3n = 7 [8]
donc 3n = 7 [8]
congruences de 3n :
n = 0[8] => 3n = 0[8]
n = 1 [8] => 3n = 3 [8]
n = 2 [8] => 3n = 6 [8]
n = 3 [8] => 3n = 1 [8]
n = 4 [8] => 3n = 12 = 4 [8]
n = 5 [8] => 3n = 15 = 7 [8]
n = 7 [8] => 3n = 5 [8]
donc si n = 1[2], alors les n tels que n*7^n + 4n + 1 divisible par 8 sotn les n congrus à 5 mod 8
2) n pair :
je te laisse étudier le cas
tu connais la formule du binôme de newton ?
Sinon, pour le dernier :
3) Déterminez les entiers naturels pour lesquels : n*7^n + 4n + 1 est divisible par 8.
on remarque que 7=(-1) [8]
donc que n*7^n = -n [8] quand n est impair
et
n*7^n = n [8] quand n est pair
deux cas donc :
1) n impair
n*7^n + 4n + 1 = 3n + 1 [8]
3n + 1 = 0 [8] 3n = -1 [8] 3n = 7 [8]
donc 3n = 7 [8]
congruences de 3n :
n = 0[8] => 3n = 0[8]
n = 1 [8] => 3n = 3 [8]
n = 2 [8] => 3n = 6 [8]
n = 3 [8] => 3n = 1 [8]
n = 4 [8] => 3n = 12 = 4 [8]
n = 5 [8] => 3n = 15 = 7 [8]
n = 7 [8] => 3n = 5 [8]
donc si n = 1[2], alors les n tels que n*7^n + 4n + 1 divisible par 8 sotn les n congrus à 5 mod 8
2) n pair :
je te laisse étudier le cas
Bonsoir !
Je me demandais, est-ce qu'un exo de ce type peut être résolu par les congruences :
Démontrer que pour un nombre entier soit divisible par 6, il faut que la somme du chiffre des unités et de quatre fois la somme des autres chiffres soit divisible par 6.
Remarquez, je me suis peut-être trompé de chapitre... :\
Merci d'avance.
Je me demandais, est-ce qu'un exo de ce type peut être résolu par les congruences :
Démontrer que pour un nombre entier soit divisible par 6, il faut que la somme du chiffre des unités et de quatre fois la somme des autres chiffres soit divisible par 6.
Remarquez, je me suis peut-être trompé de chapitre... :\
Merci d'avance.
personnellement, je te proposerai un tableau de modulo!
tout simple, tu te casse pas la tête.
tu décomposes tout tes jolies fonctions, pour la 1: n² ,- 3n, + 6
tu fais une colone pour chaque, et a la fin tu additionne, tu as ton tableau!!
Ensuite quand c'est égale à zéro tt en bas dans ton tableau c'est qu e c'est divisible!
tout simple, tu te casse pas la tête.
tu décomposes tout tes jolies fonctions, pour la 1: n² ,- 3n, + 6
tu fais une colone pour chaque, et a la fin tu additionne, tu as ton tableau!!
Ensuite quand c'est égale à zéro tt en bas dans ton tableau c'est qu e c'est divisible!
vikvik a écrit:personnellement, je te proposerai un tableau de modulo!
tout simple, tu te casse pas la tête.
tu décomposes tout tes jolies fonctions, pour la 1: n² ,- 3n, + 6
tu fais une colone pour chaque, et a la fin tu additionne, tu as ton tableau!!
Ensuite quand c'est égale à zéro tt en bas dans ton tableau c'est qu e c'est divisible!
C'est surement plus ludique. :happy2: J'essaierai.
Pour la divisibilité par 6, d'accord pour le 2 et 3, mais comment en arriver à chiffre des unité + 4 fois la somme des autres divisible par 6... ?
Pour le 3, j'utilise aussi le binôme de Newton ?
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 105 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
