Exercices
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Man_Utd
- Messages: 2
- Enregistré le: 20 Sep 2005, 14:12
-
par Man_Utd » 20 Sep 2005, 14:37
Salut,
lors de mon examen de rattrappage,j'ai eu cet exo.
Calculer la série génératrice
A(x) =
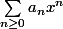
avec
et
)
je fais mon calcul
 =-2\displaystyle\sum_{n\geq0}a_{n+1}x^n-\displaystyle \sum_{n\geq0}a_{n+2}x^n+\displaystyle \sum_{n\geq0}n^2x^n-\displaystyle \sum_{n\geq0}nx^n)
=-\frac{2}{x}\displaystyle\sum_{n\geq0}a_{n+1}x^{n+1}-\frac{1}{x^2}\displaystyle \sum_{n\geq0}a_{n+2}x^{n+2}+\frac{nx}{(1-x)^2}-\frac{x}{(1-x)^2})
=-\frac{2}{x}(A(x)-1)-\frac{1}{x^2}(A(x)-1)+\frac{nx}{(1-x)^2}-\frac{x}{(1-x)^2})
etc.....
Lorsque je suis allé voir ma copie le prof m'a dit qu'il ne m'avait mis aucun point sur cet exo car à la fin du calcul de A(x) je trouvais un résultat qui dépendait de n et que si je ne comprenais pas ça remarque c'était tant pis.
Il n'a pas voulu m'expliquer.
Si quelqu'un pouvait m'expliquer et me dire comment il aurait fallu faire ce serait sympa.
Merci d'avance
-
kaya
- Membre Naturel
- Messages: 91
- Enregistré le: 03 Aoû 2005, 15:33
-
par kaya » 20 Sep 2005, 15:23
Salut!
je suis venu t'apporter une réponse assez précise de ton exo:
en fait, cet exercice traine quelquepart dans ce forum et le problème y est résolu danns les méssages mais je ne m'en souviens pas qel est son titre, donc tu n'as qu'à aller dans RECHERCHE et tu fais "recherche avancée" où tu saisira "série génératrice"
amicalement
A+
-
Galt
- Membre Rationnel
- Messages: 789
- Enregistré le: 13 Aoû 2005, 12:03
-
par Galt » 20 Sep 2005, 16:36
Dans une expression où il y a un symbole
, l'indice sur lequel porte la somme est une variable muette, qui ne doit pas apparaître dans le résultat de la somme. Dans
, par exemple, le résultat
ne contient plus les
n. Dans l'expression obtenue de A(x), le terme en
est obligatoirement faux.
-
Man_Utd
- Messages: 2
- Enregistré le: 20 Sep 2005, 14:12
-
par Man_Utd » 20 Sep 2005, 18:58
Galt a écrit:Dans une expression où il y a un symbole
, l'indice sur lequel porte la somme est une variable muette, qui ne doit pas apparaître dans le résultat de la somme. Dans
, par exemple, le résultat
ne contient plus les
n. Dans l'expression obtenue de A(x), le terme en
est obligatoirement faux.
Comment fallait-il faire pour transformer
et ainsi faire disparaitre le n qui dérange
-
Galt
- Membre Rationnel
- Messages: 789
- Enregistré le: 13 Aoû 2005, 12:03
-
par Galt » 20 Sep 2005, 19:06
Il faur revenir à
, qu'on obtient en dérivant 2 fois
donc
^2}=\sum{nx^{n-1}})
et
^2}=\sum{nx^n})
, on redérive et on obtient la somme
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
