Exercice : coordonnées vectorielles
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Rinoa_Heartilly
- Membre Naturel
- Messages: 16
- Enregistré le: 22 Oct 2007, 18:11
-
 par Rinoa_Heartilly » 22 Oct 2007, 18:17
par Rinoa_Heartilly » 22 Oct 2007, 18:17
Bonjour,
Je seche sur cet exercice que voici :
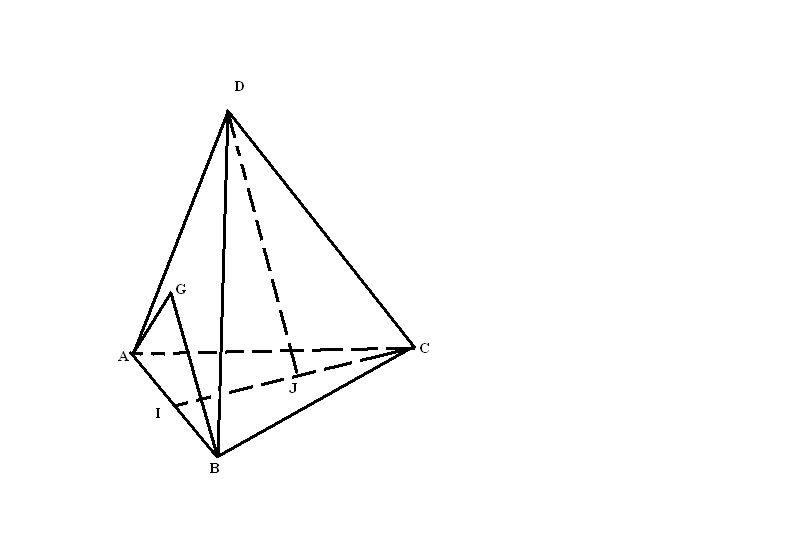
ABCD est un tétraèdre. I et J sont 2 milieux respectifs de [AB] et [IC].
G est le centre de gravité de ABD; K est un point tel que vecteur(CK) = au vecteur(3/5)(CG). Démontrer que les points D, J et K sont alignés
1.en utilisant les coordonnées et le repère (A; AB ; AC ; AD); 2. sans utiliser les coordonnées Je sais pas trop si je peux mettre une figure, si je ne peux pas je la retirerai.
C'est un simple exo (pas DM donc) mais j'y arrive vraiment pas, je vois pas comment prouver que ces 3 points sont alignés.
Merci de m'aider

-Rinoa Heartilly
-
Rinoa_Heartilly
- Membre Naturel
- Messages: 16
- Enregistré le: 22 Oct 2007, 18:11
-
 par Rinoa_Heartilly » 22 Oct 2007, 18:36
par Rinoa_Heartilly » 22 Oct 2007, 18:36
EDIT --
J'ai oublié le point K sur la figure, il se trouve à l'intersection de (DJ) et (BC).
-
Rinoa_Heartilly
- Membre Naturel
- Messages: 16
- Enregistré le: 22 Oct 2007, 18:11
-
 par Rinoa_Heartilly » 22 Oct 2007, 19:18
par Rinoa_Heartilly » 22 Oct 2007, 19:18
Re : Est-ce que mon topic n'est pas assez explicite? Car personne ne répond et j'ai quand meme besoin d'une aide (ou de la réponse lol) pour l'exercice!!!
-
Alpha
- Membre Complexe
- Messages: 2176
- Enregistré le: 21 Mai 2005, 11:00
-
 par Alpha » 22 Oct 2007, 19:24
par Alpha » 22 Oct 2007, 19:24
Si, tu as été assez explicite, mais peut-être que personne ne s'est encore penché dessus ou que personne n'a trouvé... ou n'a fait l'effort de chercher... Ca peut arriver. L'aide va peut-être venir...
-
Rinoa_Heartilly
- Membre Naturel
- Messages: 16
- Enregistré le: 22 Oct 2007, 18:11
-
 par Rinoa_Heartilly » 22 Oct 2007, 19:26
par Rinoa_Heartilly » 22 Oct 2007, 19:26
Okay, je vais donc (in)patiament et (pas) calmement... -.-
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 22 Oct 2007, 19:35
par Flodelarab » 22 Oct 2007, 19:35
Il faut utiliser les barycentres partiels.
En effet, tu peux affecter un poids à chaque point sans connaitre ses coordonnées.
En associant et dissociant des systèmes de points (accompagnés de leur poids, tu dois arriver à prouver l'alignement.
Concrètement ?
3 points sont alignés si l'un est un barycentre des 2 autres. (Hormis si les points sont confondus)
ok?
-
Rinoa_Heartilly
- Membre Naturel
- Messages: 16
- Enregistré le: 22 Oct 2007, 18:11
-
 par Rinoa_Heartilly » 22 Oct 2007, 19:40
par Rinoa_Heartilly » 22 Oct 2007, 19:40
Ouais...sauf que...j'ai pas encore vu le barycentre...O_o
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 22 Oct 2007, 19:58
par Flodelarab » 22 Oct 2007, 19:58
Rinoa_Heartilly a écrit:Ouais...sauf que...j'ai pas encore vu le barycentre...O_o
T'es pas en première ? T'es pas en train de voir les barycentres ?
alors je passe la main.
-
Rinoa_Heartilly
- Membre Naturel
- Messages: 16
- Enregistré le: 22 Oct 2007, 18:11
-
 par Rinoa_Heartilly » 22 Oct 2007, 20:01
par Rinoa_Heartilly » 22 Oct 2007, 20:01
J'ai vu ce chapitre mais pour X raison, le prof a décidé de zapper le barycentre (que j'ai néanmoins vu en physique pour des charges partielles mais pas au point de comprendre les poids)
et j'ai eu une idée, si D, J et K sont alignés, alors il suffit de prouver que J DBC, étant donné que D et K DBC?
Mais 1. je suis pas sure et 2. je sais pas comment trop faire, il était indiqué d'utiliser le repère mentionné + haut
-
Rinoa_Heartilly
- Membre Naturel
- Messages: 16
- Enregistré le: 22 Oct 2007, 18:11
-
 par Rinoa_Heartilly » 22 Oct 2007, 20:19
par Rinoa_Heartilly » 22 Oct 2007, 20:19
EDIT - Une 3e solution serait evidemment de démontrer que DJ = kDK, mais je vois pas comment :(
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 22 Oct 2007, 20:25
par Flodelarab » 22 Oct 2007, 20:25
Commence par faire la partie avec les coordonnés car tu n'as pas compris le dessin.
Aucun des points que tu me cites appartiennent à DBC de toute évidence.
Cependant, si le chapitre sur les barycentres n'est pas su, tu as raison de comparer avec la physique. C'est le même principe qu'une balance. (a plateaux multiples :lol:)
courage, potasse avec ton livre de math.
-
Rinoa_Heartilly
- Membre Naturel
- Messages: 16
- Enregistré le: 22 Oct 2007, 18:11
-
 par Rinoa_Heartilly » 22 Oct 2007, 20:30
par Rinoa_Heartilly » 22 Oct 2007, 20:30
Mais K (on le voit pas sur le dessin je l'ai oublié) est le milieu de BC et D est pas sur DBC?
O_o
Sinon comment voir pour le barycentre les "poids"? Et les exos résolus (y'en a un dans le genre du mien) me parlent de toute façon de colinéarité
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 22 Oct 2007, 20:37
par Flodelarab » 22 Oct 2007, 20:37
Rinoa_Heartilly a écrit:Mais K est le milieu de BC
Tu as rêvé cette définition.
Moi je lis que K est sur (CG) .............
-
Rinoa_Heartilly
- Membre Naturel
- Messages: 16
- Enregistré le: 22 Oct 2007, 18:11
-
 par Rinoa_Heartilly » 22 Oct 2007, 20:38
par Rinoa_Heartilly » 22 Oct 2007, 20:38
Oh evidemment...Si déjà je pars de la mauvaise hypothèse...
Mais ça ne clarifie pas plus mon esprit O_o
-
Rinoa_Heartilly
- Membre Naturel
- Messages: 16
- Enregistré le: 22 Oct 2007, 18:11
-
 par Rinoa_Heartilly » 22 Oct 2007, 20:52
par Rinoa_Heartilly » 22 Oct 2007, 20:52
Re-Edit : Ca fait maintenant3h que je bosse et la franchement je peux plus attendre (il est 11h), y'a pas qualqu'un qui peut me passer la solution? J'ai essayé de le résoudre mais là je ne peux franchement plus attendre, en plus demain il se peut qu'il les ramasses les exos...
:briques: :briques: :cry: :triste: :hum:
-
Rinoa_Heartilly
- Membre Naturel
- Messages: 16
- Enregistré le: 22 Oct 2007, 18:11
-
 par Rinoa_Heartilly » 22 Oct 2007, 21:06
par Rinoa_Heartilly » 22 Oct 2007, 21:06
Plus que quelques minutes avant que je me deconnectes :cry: la je vais surement me faire tuer ... vraiment personne peut me dire la solution, j'ai enocre pleins de matières à bosser après :cry:
(et si on pouvait me dire ou se trouve le bouton pour Editer, je l'avait trouvé mais il s'est barré lol)
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 22 Oct 2007, 23:33
par Flodelarab » 22 Oct 2007, 23:33
Par définition de K:

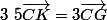
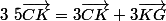
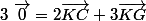
K est le barycentre de {(C;2)(G;3)}
K est le barycentre de {(C;2)(A;1)(B;1)(D;1)} car G barycentre de {(A;1)(B;1)(D;1)}
K est le barycentre de {(C;2)(I;2)(D;1)} car I barycentre de {(A;1)(B;1)}
K est le barycentre de {(J;4)(D;1)} car J barycentre de {(C;2)(I;2)}
Conclusion: K, J, D sont alignés.
On sait même que DK=4KJ (ce sont bien des longueurs)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 82 invités

