Faiblement derivale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
smooth5185
- Membre Naturel
- Messages: 21
- Enregistré le: 21 Oct 2007, 12:04
-
 par smooth5185 » 21 Oct 2007, 12:12
par smooth5185 » 21 Oct 2007, 12:12
Bonjour a tous,
au fait j'ai un probleme d'application du theoreme de la derivée faible:
En effet comment montrer que la fonction f(x) = |x| est faiblement derivable, et ainsi calculer sa derivee faible?
Merci beaucoup et a bientot. :we:
-
smooth5185
- Membre Naturel
- Messages: 21
- Enregistré le: 21 Oct 2007, 12:04
-
 par smooth5185 » 21 Oct 2007, 12:14
par smooth5185 » 21 Oct 2007, 12:14
En fait je pense qu'il faudrait trouver la fct f' appartenant a L1,loc qui verifirai la definition.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 21 Oct 2007, 12:26
par tize » 21 Oct 2007, 12:26
Bonjour,
il me semble que la dérivée faible est
=\left{\matrix 1.. si x\geq 0\\-1.. sinon\matrix)
.
Elle vérifie pour tout


à support compact :
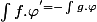
-
smooth5185
- Membre Naturel
- Messages: 21
- Enregistré le: 21 Oct 2007, 12:04
-
 par smooth5185 » 21 Oct 2007, 14:15
par smooth5185 » 21 Oct 2007, 14:15
ouai je pense que c'est bien ca,
merci bien
par contre j'ai un autre probleme:
Montrer que la fonction de Heaviside (fonction indicatrice de R+) est faiblement derivable?
ie que l'on peut montrer qu'elle appartient a Hs(R) mais comment ?
Merci
-
rifly01
- Membre Relatif
- Messages: 460
- Enregistré le: 30 Déc 2005, 04:38
-
 par rifly01 » 21 Oct 2007, 14:51
par rifly01 » 21 Oct 2007, 14:51
Bonjour,
Une forme condensée :
=\frac{x}{|x|})
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 21 Oct 2007, 14:58
par tize » 21 Oct 2007, 14:58
Je pense plutôt que c'est le Delta de Dirac :

-
smooth5185
- Membre Naturel
- Messages: 21
- Enregistré le: 21 Oct 2007, 12:04
-
 par smooth5185 » 21 Oct 2007, 15:08
par smooth5185 » 21 Oct 2007, 15:08
ok merci,
mais comment faire pour mq la fct indicatrice de1 R+ est faiblement derivable ?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 21 Oct 2007, 15:28
par tize » 21 Oct 2007, 15:28
Soit


a support compact dans
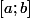
.
\varphi'(x)dx=\int_0^b \varphi'(x)dx)
si b>0 sinon ça fait 0.
Donc :
\varphi'(x)dx=\int_0^b \varphi'(x)dx=\varphi(b)-\varphi(0)=-\varphi(0))
car
=0)
or
=-\int\delta\varphi)
-
smooth5185
- Membre Naturel
- Messages: 21
- Enregistré le: 21 Oct 2007, 12:04
-
 par smooth5185 » 21 Oct 2007, 15:34
par smooth5185 » 21 Oct 2007, 15:34
ok j'ai bien compris ton raisonnement mais juste pk fi(b)=0 ?
merci.
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 21 Oct 2007, 15:47
par kazeriahm » 21 Oct 2007, 15:47
parce que phi s'annule en dehors de [a,b] et est continue
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
