Polynôme caracteristique

[Baby Dear]

Bonsoir



J'ai un petit problème en maths. Je ne comprend pas pourquoi

;)u (u)(x) ,où ;)u est le polynôme caracteristique de u pour u appartenant à L(E), est nulle lorsque x égal zéro. Pour moi ;)u (u)(x)=det(u-u(x)Id) donc pour x=0 on devrait avoir ;)u (u)(0)=det(u) et det(u) n’est pas necessairement nul….

[ThSQ]

;)u (u)(0)=det(u)

det(u)*Id(x) avec x=0 plutôt ce qui devrait résoudre ton problème

[Skullkid]

Bonsoir, tu confonds en fait deux notions différentes : les polynômes (éléments de 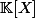) et les polynômes d'endomorphismes (éléments de ).

est bien défini, c'est le déterminant de l'application linéaire Xid-u (l'indéterminée X a vocation à représenter un scalaire quand on passe à la fonction polynômiale associée).

Par contre, écrire n'a aucun sens : u(x)id serait le produit d'un vecteur par une application, ce qui n'est pas défini.

Si on pose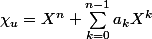 , ce qu'on note c'est l'endomorphisme 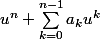, et donc , qui est bien nul quand x est le vecteur nul.

est d'ailleurs nul pour tout x, par le théorème de Cayley-Hamilton. D'ailleurs, ce théorème semble évident si on ne remarque pas la confusion que tu as faite (en version matricielle) : , ce qui est évidemment faux (même si le résultat est juste).