Mouvement Brownien

[tonythx]

Voici un problème de processus stochastique qui me pose bien des problèmes!

Soit ( ) un mouvement brownien et soit >0 fixé.
Prouver que (C := - )
est aussi un mouvement brownien

Je vous serais infiniment reconnaissant si vous pouviez m'aider, au moins me donner une piste.

Merci beaucoup

[AngeBlanc]

Si tu me définis ce qu'est le mouvement brownien en termes mathématiques, je veux bien...

[BQss]

Salut,

il faut revenir a une des deux definitions, ici le plus rapide(quoi que, l'autre est assez triviale aussi):


il faut montrer que:

1) est t-continue p.s:

or B est t-continue p.s en tant que mb, donc C l'est aussi comme difference.

2)Les accroissements st indépendants(prenons une suite quelconque):



par ailleurs (pour et tout autres accroissements disjoints):


qui par l'a.i de B(ceux de B le sont pour toute suite t_n ) forment des accroissements indépendants et on obtient ainsi celle de C.

3) sui la loi N(0,t-s):


qui suit la loi car B est un mouvemment brownien(du a la definition).

4):

...


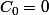
Mais il y a au moins une autre facon(en utilisant la covariance et qu'un mvmt brownien est aussi un processus gaussien, je parie que ton prof utilisera la version covariance plus calculatoire et qui suppose deja admis certains resultats, comme ). Il faut je pense que tu revois un peu ton cours, car c'est la base .

[tonythx]

Merci infiniment, tu m'a donné exactement ce que je cherchais, et on n'a pas vu ce dont tu parles pour la deuxième solution.

Pour répondre à Ange Blanc :
Un mvt brownien est un processus stochastique à valeurs réelles qui est un processus à accroissement indépendant et stationnaire et dont les trajectoires sont continues presque surement. (cf. cour)

Merci de votre attention.

[BQss]

"et stationnaire "

stationnaire et qui suivent(pour tout accroissement )une loi N(0,t-s).
Car tu peux tres bien avoir des processus ayant les memes propriétés mais ou les accroissements suivent une autre loi.

La definition la plus large de ce genre de processus est en fait celle d'un PAIS:
"processus a accroisssements indépendants, stationnaires" , continue a droite(ce qui permet d'englober les processus a sauts, qui bien que discontinues, sont continues a droite) et tel que .

exemple un processus de poisson de parametre est un PAIS ou les accroissements ont pour loi P( (avec P la loi de poisson). Un processus de poisson est bien continue a droite ( par ailleurs les temps d'attente entre ses sauts suivent une loi exponentielle).