Droite 3D connaissant deux points

[totor]

bonjour,

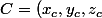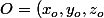j'aimerais trouver l'équation d'une droite dans connaissant deux points, et . Apparement j'ai lu que c'est l'intersection de deux équations du plan, du style :



mais est-il possible de résoudre ce système pour trouver les coefficents a,b,c,d ... il n'y a pas assez d'équations, non ?


merci par avance

[chan79]

Bonjour
S'il s'agit de trouver les équations de deux plans passant par une droite (définie par deux points) il y a une infinité de solutions...
A priori pense à:
M est un point de (AB) s'il existe un nombre k tel que vec(AM)=k.vec(AB)

[totor]

Bonjour
S'il s'agit de trouver les équations de deux plans passant par une droite (définie par deux points) il y a une infinité de solutions...
A priori pense à:
M est un point de (AB) s'il existe un nombre k tel que vec(AM)=k.vec(AB)

salut,
merci pour ta réponse, j'avais l'impression qu'on pouvait tracer une unique droite entre deux points 3D, non ? C'est ce que je chercherais à faire ...

[chan79]

tu peux résoudre
axc+byc=-czc;)d
axo+byo=-czo;)d

en donnant des valeurs arbitraires à c et d; tu auras a et b
je te conseille de prendre un exemple numérique C(1;2;3) et O(5;2;4)

sinon par deux points il passe une infinité de plan
pense à une porte qui pivote autour d'un de ses côtés; chaque position de la porte est un plan qui passe par l'axe de rotation