Convergence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Mohamed
- Membre Relatif
- Messages: 225
- Enregistré le: 02 Juil 2006, 21:01
-
 par Mohamed » 13 Oct 2007, 21:39
par Mohamed » 13 Oct 2007, 21:39
Bonsoir...
en fait j'ai deux petites questions :
1.pour f continue ,u_n et v_n deux suites , dans quels cas on a
)=f(u_n)+o(v_n))
?
pour la deuxième, je vois pas comment déterminer la nature de la série de terme général :
^k}{n})
ou k =[sqrt(n^2+1)]
[.] est la partie entière
merci d'avance
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 13 Oct 2007, 21:58
par aviateurpilot » 13 Oct 2007, 21:58
tu parle de la serie
^{[\sqrt{n^2+1}]}}{n}=\bigsum_{n\ge 0}\frac{(-1)^{n}}{n})
c'est facile si tu veux bien dire
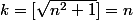
-
Mohamed
- Membre Relatif
- Messages: 225
- Enregistré le: 02 Juil 2006, 21:01
-
 par Mohamed » 13 Oct 2007, 22:02
par Mohamed » 13 Oct 2007, 22:02
k=[sqrt(n)], c'était une erreur...
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 13 Oct 2007, 23:01
par aviateurpilot » 13 Oct 2007, 23:01
soit
^{[\sqrt{i}]}}{i})
on a
^2-1}-S_{(2n)^2}=\bigsum_{k=(2n)^2}^{(2n+1)^2-1}\frac{1}{k}<\frac{4n+1}{(2n)^2})
et
^2-1}-S_{(2n+1)^2}=\bigsum_{k=(2n+1)^2+1}^{(2n+2)^2-1}\frac{-1}{k}<\frac{-(4n+3)}{(2n+2)^2})
donc
=S_{(2n+2)^2}-S_{(2n)^2}<\frac{1-(4n+3)}{(2n+2)^2}+\frac{4n+1}{(2n)^2}-\frac{1}{(2n+1)^2}\le \frac{6/4}{n^2})
mtn est tres facile de montrer que

est majorée
d'ou la convergence de ta suite (sauf erreur de mes calcules)
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 14 Oct 2007, 09:16
par ThSQ » 14 Oct 2007, 09:16
Chuis pas bien réveillé mais il me semble bien que

et donc
 = n)
???
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités