Racine Enième d'un réel

[Clark_]

Hello!

J'ai un cours qui me dit que les racines n-ième d'un complexe a+ib=z quelconque sont de la forme:
(|z|^1/n)e^(i(2kPi+TETA)/n), avec k appartenant à l'ensemble [0; n-1], et téta l'angle du complexe en question.

Qu'en est t'il pour les réels?
Genre si je pose: u^3=27. Une solution est (clairement) 3, mais les autres? On m'a dit que les autres solutions étaient de la forme "une solution particulière + e^(i2kPI/3), k dans [0; n-1] pour ce cas là par exemple, mais y'a un pépin, car en dévellopant le cube, on tombe pas sur 27... Donc c'est faux
Bref?

[yos]

Tout réel est un complexe donc ça marche.
Que fait ce + là où il y a un X ???

[busard_des_roseaux]

concernant les réels:

1) pour n impair,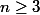
la fonction est une bijection bicontinue, strictement croissante de 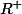sur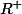
Quelque soit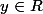 , l'équation d'inconnue x:
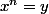a une solution unique notée

la fonction est continue mais non dérivable en y=0.

2) pour n pair, il faut se restreindre à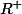 pour avoir un résultat
semblable. cf, la racine carrée.

euh, je suis hors sujet. désolé.

[xyz1975]

Bonsoir
Tout réel est complexe, dans le cas où le mebre gauche est réel deux question peuvent se poser :
On cherche les racines nièmes dans R ou dans C, si c'est dans C le problème est résolu C étant un corps algébriquement clos donc il existe n racines. dans le cas où on cherche les racines nièmes dans R là les choses passent très mal.
Prenez l'exemple z^3=1 ou z^4=2 dans R.