Suites

[euclide]

Bonjour à tous, on a :

des nombres complexes et la suite définie par récurrence de la façon suivante :



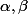
On considère de plus les racines que l'on suppose distinctes, de l'équation suivante :



Il faut montrer que l'on a deux nombre A et B tels que :

[abcd22]

Bonjour,
Quelle est la dimension de l'ensemble des suites qui vérifient la relation de récurrence ? (combien faut-il d'éléments d'une de ces suites pour la déterminer entièrement ?). Une fois qu'on a la dimension de l'espace il n'y a plus qu'à en trouver une base...

[euclide]

Je pense que deux éléments suffisent à la déterminer entièrement. Mais comment trouver une base ?

[euclide]

J'ai pensé à considérer la matrice suivante , parce-qu'on a :

et donc

de plus de cette façon et sont les valeurs propres de la matrice. On peut donc peut-être diagonaliser la matrice pour avoir une expression de sa n ème puissance. Qu'en pensez-vous ?

[abcd22]

Ça doit marcher avec les matrices, sinon pour la base ben les deux suites sont données dans l'énoncé...

[euclide]

Les deux suites sont ?

[abcd22]

Oui, il faut prouver qu'elles vérifient bien la récurrence et qu'elles forment une famille libre.

[euclide]

D'accord, je vois comment montrer qu'elles vérifient la récurrence et comment montrer qu'elles forment une famille libre. Je comprend donc pour la suite (an) peut s'écrire sous cette forme, mais comment fait-on pour déterminer les constantes A et B ?

[abcd22]

On utilise les valeurs a_0 = A
+
B et a_1 = ..., mais le calcul général n'a pas grand intérêt...