Sous-Groupes !

[birdy01]

Bonjour à tous !
Je suis entrain de réviser les sous-groupes et je ne comprend pas bien une notation. :marteau:
Dans un exercice, on me demande de démontrer que nZ est un sous-groupe de R.
Comment démontrer que c'est une LCI (pardon : Loi de composition interne) ? :mur:
Je bloque, merci de votre aide

[legeniedesalpages]

C'est quoi une LCI?

[birdy01]

désolé, LCI c'est une loi de composition interne

[legeniedesalpages]

oui mais je sais bien, c'est quoi sa définition?

La mienne c'est pour notre cas



C'est donc la restriction de




Il y a donc juste à montrer que est à valeurs dans et tu auras une LCI.

[birdy01]

La notation me dérange, dans mon cours j'ai :
* est une lci sur E si :
- E non vide
- * est une application de ExE dans E.

Et un groupe est noté (E,*). Dans l'enoncé, il y a juste R

C'est un peu brouillon dans ma tête ! :hum:

[legeniedesalpages]

c'est ce qu'on dit en général.

en fait dans le dernier post, je t'ai dit que la loi est la restriction de la loi 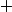de .

Pour finir de la montrer, il faut que tu montres que pour tout , .

Mais bon ça te montrera pas que c'est un sous-groupe de , pour le montrer il faut que tu vérifies (d'après la définition d'un sous groupe) que:

i) ,
ii) , quels que soient ,
et
ii) , quelque soit .

[legeniedesalpages]

Et un groupe est noté (E,*). Dans l'enoncé, il y a juste R

On sous-entend .
Quand il n'y a pas ambiguité sur la loi, on note E au lieu de (E,*).

[birdy01]

Ah ça se précise ! :we:
Mais pourquoi + et pas . ?

[legeniedesalpages]

On a du te faire remarquer que n'est pas un groupe (0 n'est pas inversible), donc il n'y a vraiment d'autres possibilités que .

[birdy01]

Merci beaucoup ! Je commence à comprendre. Je vais essayer de relire le cours et d'en comprendre toutes les petites finesses et ensuite je tenterais de faire l'exercice en suivant tes conseils.
Merci :ptdr: :ptdr: